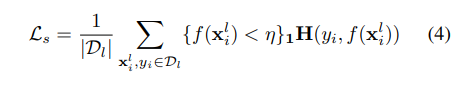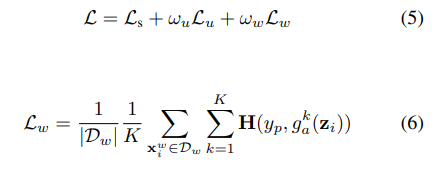오늘 정리할 논문은  AAAI'22에 accept 된 guidedmix-net이다. 
semi supervised learning으로 segmentation 성능 개선 방법은 제안 한다.
 
title: GuidedMix-Net: Semi-Supervised Semantic segmentation by using Labeled Image as Reference

 official repo:https://github.com/yh-pengtu/GuidedMix-Net/tree/main

문제 제기:

기존 제안된 방식은 unlabeled data를 모델의 consistency만을 강화하는 방식으로 사용해 왔고 이는 unlabeled data로 부터 얻을 수 있는 많은 양의 prior knowledge 를 활용하지 못하는 방식이다.
 
1. 학습시 labeled data와 unlabeled data 를 분리해서 따로 사용하고 unlabeled data 는 다양한 manual perturbation 을 이용해 consistency 학습에만 사용
-> 이런 방식으로는 unlabeled data 가 가지는 정보를 모두 활용 하지 못하고 이는 모델이 sub optimal(local minima)에 도달하는 결과를 초래할 수 있다.
2. CCT와 같은 방식은 다양한 perturbation을 생성해 consistency를 학습하는 방식이기 때문에 학습 시간이 오래걸릴 수 있음
 
아래 Figure 1. (c)를 보면 CCT 로 생성한 pseudo mask 는 부정확 한데 본 논문의 저자들은 이것을 자신들의 주장을 뒷바침 하는 근거로 제시한다. 

Proposed method

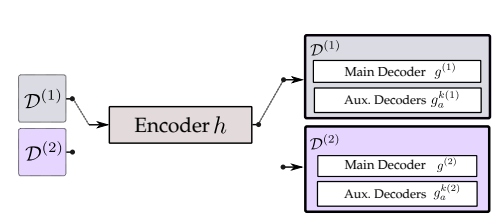
GuidedMix-Net에서는 labeled data 의 정보를 unlabeled data 에 전달해 학습을 guide 하는 방법을 제안하고 이를  mutual information transfer 라 하고 전체 아키텍쳐는 아래 그림과 같다. 
(우선 이 그림엔 틀린 부분이 있는것으로 보이는데 official code 를 보면 parameter sharing 이 되는 부분은 Figure 2 의 붉은 색으로 표시된 encoder 부분만 이다. decoder 는 labeled data만 이용해 학습 하는 decoder 와 mix input을 이용해 학습하는 decoder가 서로 다르다.)
 

labeled data의 정보를 이용해 unlabeled data을 이용한 학습을 guide 하기 위해 이논문에서는 3step process 를 제안한다. 

1. labeled-unlabeled pair interpolation

2. Mutual information transfer

3. pseudo mask generation

Labeled-unlabeled pair interpolation

이 단계는 labeled image ($x^{i}_{l}$) 와 unlabeled image($x^{j}_{u}$)을 혼합하해 Figure 2 의 아래쪽 입력에 해당하는 혼합이미지 $x^{j}_{mix}$를 생성하는 단계이다. 

혼합 이미지를 생성하는 방법은 위와 같다. labeled image ($x^{i}_{l}$) 와 unlabeled image($x^{j}_{u}$)를 $\lambda$ 비율로 더하는 과정이 전부이다. $\lambda \in (0,1)$ 로 $Beta(\alpha, \alpha), \alpha=1$ 로 부터 생성하고 $\lambda=min(\lambda, 1-\lambda)$ 와 같이 설정한다. 

이때 랜덤으로 labeled-unlabeled image pair를 선택하는 것보다 유사 이미지를 선택하는 것이 더 효과적이라고 하는데 그 이유는 동일/유사한 object 를 포함한 두 이미지가 섞여야 labeled image 로 부터의 정보가 unlabeled image 로 전파 더 잘 전파 될 수 있기 때문이다. 유사 이미지를 선택하는 방법은 mini batch 내에서 encoder의 output 으로부터 계산한 euclidean distance 가 가장 작은 labeled-unlabaled image 쌍을 선택하는 것이다. 아래 식에서 $\Gamma$ 는 model의 encoder 를 의미한다.

 한가지 트릭으로 이 방식으로 유사한 이미지 쌍을 선택하기 위해 encoder에 fullly connected layer 를 추가해 classification network을 만들고 labeled image만을 이용해 네트워크를 미리 트래이닝 시켜 비슷 한 이미지들이 feature space에서 유사한 위치에 있도록 한다. 

이를 코드로 나타내면 아래와 같다. Official repo에서 발췌한 건데 mini batch 내에서 유사한 이미지를 선택하는 부분은 빠져 있고 mini batch random image pair를 만드는 방식이다. 또한 가지 Figure 2에서와 다른 부분은 $x_{mix}$를 생성할 때 사용 되는 것은 실제 입력 이미지가 아니라 encoder의 output 에 해당한 feature map 이라는 것이다. 

lam = np.random.beta(alpha, alpha)
lam = min(lam, 1-lam)
while lam >= self.lambda_factor:
    lam = np.random.beta(alpha, alpha)
    lam = min(lam, 1-lam)

indices = torch.randperm(img.size(0), device=img.device, dtype=torch.long)
feats_mixed = lam * feats_aspp_labeled + (1-lam) * feats_aspp_unlabeled[indices]

Mutual information transfer

단순히 labeled-unlabeled image 를 interpolation 하는 것 만으로는 labeled image의 신뢰할 수 있는 정보(labeled 이 있기때문에 이렇게 표현한 것 같다)가 unlabeled image로 흐르는 것이 제한 적이기 때문에 이를 보완 할 방법으로 non-local block을 제안한다. 

 왜 단순 pairing 만으로 신뢰할 수 잇는 정보의 전파가 안되는 것일까? 이건 convolution filter의 특징때문으로 볼 수 있다. convolution filter 는 지역성을 가진다. 따라서 pairing된 이미지에서 같은 class에 속한 object 가 서로 유사한 위치에 있을 때(short-range)는 convolution만으로도 labeled image의 정보가 unlabeled image 로 흐를 수 있지만  mixed 된 이미지에서 정보를 전달할 object들이 서로 원거리에 있다면(long-range) 단순 convolution연산 만으로는 이 논문에서 원하는 효과가 제한적이다. 

그래서 이 논문에서는 non-local block을 사용 했다. Figure 3 의 블러도만 봐도 단적으로 안수 있듯이 self-attention과 같은 역할을 하는 non-local block을 이용해 long-range 정보를 전달하겠다는 전략이다. (self-attention 은 임의의 두 포인트의 interaction을 계산하기 때문에 long range dependency를 직접적으로 계산할 수 있다.)

논문에서는 이 모듈을 MITrans 라 명명 하는데 Mutual Information Transfer 이라는 의미이다.

왜 이 블럭이 labeled image 의 정보를 이용해 unlabled-image의 학습을 가이드 할 수 있다고 주장하는 것인지 의문이 들수 있는데 간단히 생각해 보자. labeled image를 이용해 supervised learning 을 진행 하므로 labeled image 가 encoder 를 거쳐 생성 되는 feature map에 있는 정보는 꽤나 신뢰 할 만 한 각 class 에 속하는 pixel들의 정보라 할 수 있다.  이 feature 과의 convolution 연산 이나 self-attention 연산을 거쳤을 때 그 response 가 크면 smoothness assumption 에 의해 유사한 feature 라고 볼 있다. 작으면 유사하지 않은 feature 라고 볼 수 있다. unlabeled image 로 부터 추출한 feature 가 labeled image로 부터 추출한 feature를 통해 correction 되는 효과를 기대할 수 있다는 것이다. 이 때문에 mutual information transfer라고 이 개념을 설명 한다. 

한가지 정말 맘에 드는 것은 MITrans block은 모델을 학습 할때만 사용 된다. 단순 inference time에는 이 블럭이 사용되지 않는다. 이게 왜 중요한 부분인지 edge device에서 서비스를 해본 사람은 이해 할 수 있을 것이다. (23년 기준..). Edge device의 경우 chip vender에 따라 self attention에 필요 한 연산을 지원하는 sdk를 아직 배포 하지 않는 곳도 있고 오래된 sdk version을 사용 하는 경우 self attention 을 inference time에 사용하는게 불가능 한 경우가 있기 때문이다. 

중요한 블럭인것은 맞지만 Figure 3 만 봐도 의도를 직관적으로 파악 할 수 있으므로 수식을 생략한다.

pseudo mask generation

마지막으로 labeled-unlabeled image pair 를 이용해 생성한 $x_{mix}$ 를  MITrans 에 통과 시킨후 decoder 를 통해 생성한 segmentation mask 는 labeled image에 존재하는 object에 해당하는 부분이 존재한다.

이 부분은 unlabeled image의 pseudo gt 로 사용 하기에 필요 없을 뿐더러 해당 부분에 대한 정확한 정보는 labeled image 의 GT를 이용해 supervised learning process(Figure 1의 윗 부분)에서 학습 되므로 필요가 없다. 

 이러한 이유로 이 논문에서는 mixed image를 이용해 생성한 pseudo mask 에서 labeled image 에 해당 하는 부분와 unlabeled image 에 해당 하는 부분을 분리 하는 방법(decoupling method)을 생각해 냈다.  방법 자체는 아주 단순하고 직관적이다.  mixed image를 네트워크에 통과시켜 얻은 prediciton 에서 labeled image를 네트워크에 통과시켜 얻은 prediction 을 빼는 것이다. 

 왜 이렇게 한 것일까? mixed image는 labeled/unlabeled image의 가중 합으로 생성된 것이므로 mixed image를 네트워크에 통과시켜 나온 prediction은 labeled image와 unlabeled image 를 네트워크에 각각 통과시켜 나온 prediction $M_{l}, M_{u}$ 을 더한 것과 유사할 것이라는 가정에서 시작 된다.  

수식으로 표현 하자면 아래와 같다. 

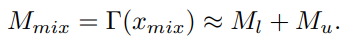
여기서 $\Gamma$는 segmentation network을 나타내고 $M_{l},M_{u}$는 각각  labeled image , unlabeled image의 prediction 에 대응 된다. 

저자는 hard decoupling과 soft decoupling  두 가지를 테스트 해봤는데 soft-decoupling 이 결과는 더 좋았다. 

hard decoupling  

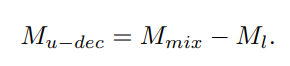
Hard decoupling 은 정말 mixed image와 labeled image의 prediction을 단순 뺄샘한다.  하지만 mixed image를 생성 할때 

$x_{mix} = \lambda x_{l} + (1-\lambda)x_{u}$ 와 같이 두 이미지를 weighted sum  하기 때문에 이는 적절하지 않아 보인다. 

Soft decoupling

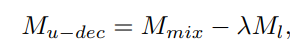
soft decoupling은 입력인 mixed image를 생성할 때 사용했던 weight $\lambda$를 고려해 위와 같이 pseudo mask 를 생성한다. soft decoupling을 사용 할때 얻을 수 있는 장점은 같은 class에 속한 object 가 labeled, unlabeled image 의 동일 한 위치에 있을때 labeled image prediction 을 mixed image prediction 에서 빼도 unlabeled image object에 대한 추론 정보가 남아있다는 것이다. 

위와 같이 생성된 psedu mask $M_{u-dec}$는 unlabeled image의 pseudo GT 로 활용하며 unlabeled image의 loss는 아래와 같이 mean squred error로 계산 된다. 

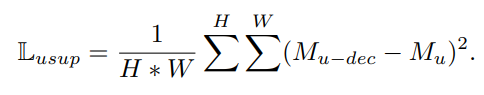
$M_{u-dec}$ 는 soft-decoupling 또는 hard decoupling 을 통해 생성한 pseudo mask 이고 $M_{u}$ 는 unlabeled image의 prediction 결과 이다. 

Loss

GuidedMix-Net 의 loss function 은 아래와 같다. 

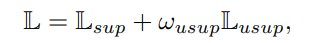
$L_{usup} 은 바로 이전에 unlabeled image의 loss 이고 $\omega$ 는 unsupervised loss weight 으로 하이퍼 파라미터이다. 

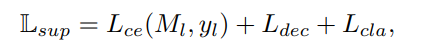
$L_{sup}$는 labeled image의 superised loss 이다. 직관 적으로 알 수 있듯이 $L_{ce}$ 는 labeled image의 cross entropy이고 $L_{cla}$는 image level의 classification loss 이다. 이전 섹션인 proposed method의 similar image selection 을 위해 encoder에 fully connected layer 를 추가해 classification network 을 학습 시킨다고 했는데 이 부분에 해당하는 loss 이다. 

$L_{dec}$ 에 대한 아래 부분은 설명이 틀릴 수 있음을 밝힌다. 코드 상에서 해당 하는 부분을 정확히 파악 할 수 없어 정확한 의미 파악이 힘들다. 틀린 부분은 지적바란다. 

$L_{dec}는 labeled image의 consistency loss term 으로 볼 수 있다. labeled-unlabeled image pair 를 이용해 mixed image를 생성했던 것을 그대로 labeled-labeled image pair 에 적용해 mixed image 를 생성한다. (단 여기서 labeled image pair 에 속한 두 장의 이미지는 같은 이미지인것으로 보인다.)

$\hat{x_{l}}, x_{l}$가 모두 labeled image 일때  $x^{l}_{mix}= \lambda x_{l} + (1-\lambda)\hat{x_{l}}$과 같이 생성한다. 이를 network에 통과시켜 prediction $M_{mix}$를 얻는다. 그 후 labeled-unlabeled image pair의 prediction decoupling 방법을 여기에 적용한다. $M_{dec}=M_{mix} -M_{l}$  여기서 M_{l}은 labeld image $x_{l}$의 prediction 이다. 

이렇게 구한 $M_{dec}$ 를 이용해 아래와 같이 구한다. 

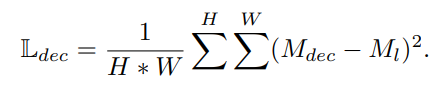
Result 

Table 1은 $\lambda$ 값의 변화가 성능에 미치는 영향을 보여준다. $\lambda$ 의 제한 범위에 따라 성능이 굉장히 상이 하니 참조 하자. 

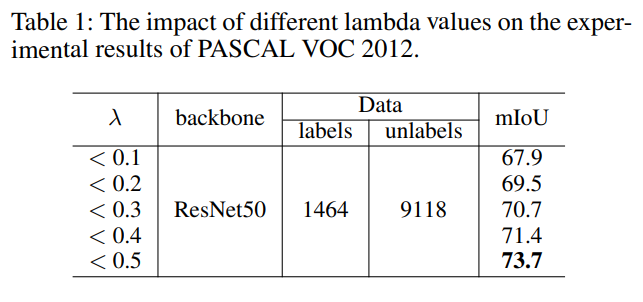
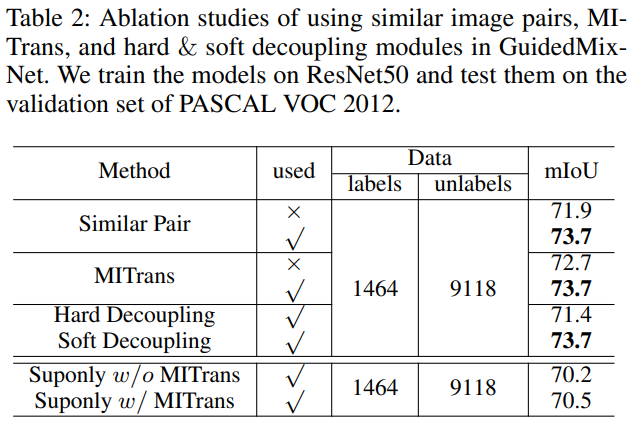
Table 2는 similar labeled-unlabeled image pair selection, MITrans(mutual information transfer) block, hard/soft decoupling 의 적용에 따른 결과를 보여 준다. 

labeled-unlabeled image pair selection 의 경우 random selection 보다 eclidean distance 를 이용한 silimar image pair selection 을 할 경우 성능이 더 좋았다. MUTrans block 도 사용하는 경우 성능이 더 좋았다. Hard decoupling 보다는 soft decoupling 을 사용하는게 더 성능이 좋았다. 

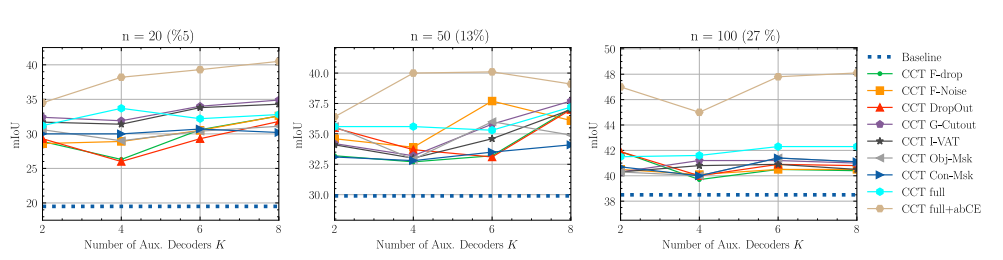
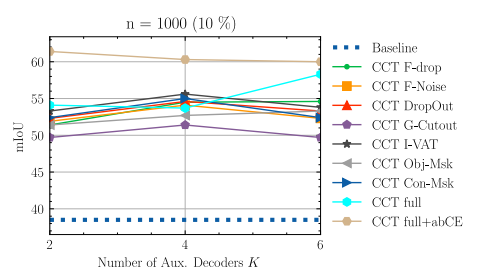
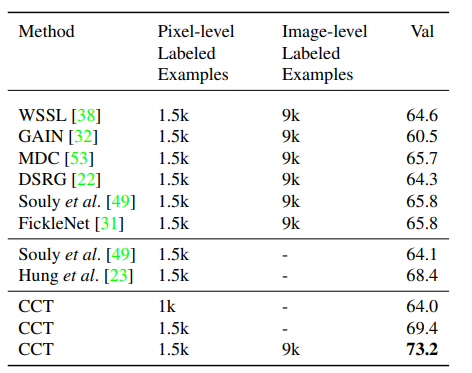
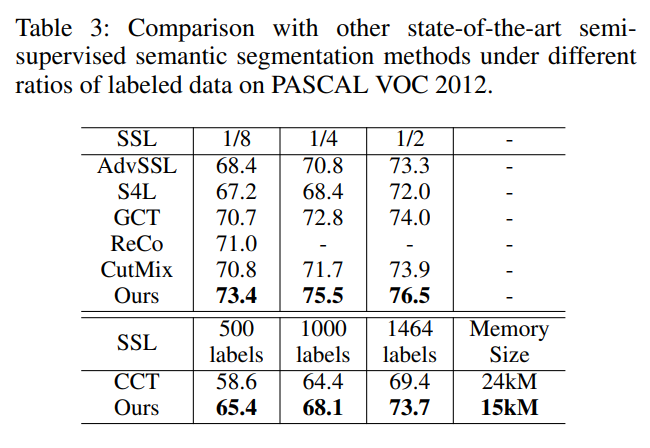
다음으로 다른 SOTA 들과의 비교이다. 다른 semi supervised learning 기반 방식들 보다도 동일한 비율의 labeled 데이터를 사용 했을 때 더 좋은 성능을 보였고 개인적으로 인상깊은 것은 이전에 읽은 논문인 CCT와의 비교 였다. 

CCT대비 큰 성능 이득을 보여 주는게 인상적이었다. 내 데이터 셋에 적용해 비교해 봐야겠다. 

-끝-

이 포스팅에는 semi-supervised learning이 동작하는데 필요한 전제 조건 또는 가정에 대해 정리한다.
내용은 mit press semi supervised learning을 참고 했다.

semi supervised learning을 왜 사용하는가?
semi-supervised learning의 주목적은 단순한 질문에서 시작된다.

"label이 존재하는 데이터만 사용하는 것과 비교했을때 unlabeled data points를 이용해 더 정확한 예측을 할수 있을까?"

이론적으로 답은 당연히 "yes"이다.  다만 여기엔 전제 조건이 있고 지금 부터 그 전제 조건들을 정리해보자.

수학적으로 위 문장을 표현해 보자면 unlabeled data로 부터 얻은 random variable x에 대한 지식 $p(x)$가 조건부 확률 $p(y|x)의 추정에 도움이 될때 semi-supervised learning은 효과가 있다.  이 전제가 깨지면 semi-supervised learning은 의미가 없다.

Semi-supervised smoothness assumption

if two points $x_{1}, x_{2}$ in a high-density region are close, then so should be the corresponding outputs $y_{1}, y_{2}$ 

말인 즉 "데이터 x_{1}, x_{2}가  데이터 공간상에서 가까운 거리에 있다면 그 대응 되는 출력(outputs이라고 되어 있는데 예측(=prediction) 값을 말한다)도 예측 공간상에서 가까운 거리에 위치 해야 한다"는 의미이다.

다른 말로 하면 비슷한 입력에 대해 비슷한 출력을 갖는다는 것이다. 즉, 데이터 공간에서 인접한 점들은 유사한 레이블을 갖는 경향이 있다는 것이다.

Smoothness assumption은 레이블이 없는 데이터를 활용하여 결정 경계(decision boundary)를 부드럽게 만드는 데 도움을 준다. 즉, 레이블이 있는 데이터에 대한 정보를 기반으로 레이블이 없는 데이터를 예측하는 과정에서, smoothness assumption에 따라 이웃하는 데이터의 레이블 정보를 활용하여 결정 경계를 조정하거나 보완하는 것이다

Cluster assumption

If points are in the same cluster, they are likely to be of the same class

데이터가 같은 클러스터에 속한다면 같은 클래스에 속할 것이다. 라는 뜻으로 매우 합리적으로 보인다.
이 가정이 어떻게 semi-supervised learning을 지지하는 가정일까?
입력 데이터가 데이터 공간에서 cluster를 형성한다고 가정해 보자. 그렇다면 입력 데이터 공간에서 clustering 알고리즘을 이용해 cluster를 분리 하고 labeled data를 이용해 각 cluster에 class를 부여 할 수 있다. 이 과정에서 데이터 공간상의 unlabeled data를 이용한다면 각 cluster의 경계를 더 잘 구분할 수 있을 것이다. 왜냐면 unlabeled data까지 활용 한다면 각 cluster에 속한 데이터의 분포를 더 정확히 추정할 수 있고 이는 곳 더 정확한 cluter 사이의 경계 추정을 할 수 있다는 의미 이기 때문이다.

여기서 한 가지  당연한 질문을 생각 할 수 있는데 "그럼 클러스터의 경계는 어디에 형성되는가?" 이다.  
답은 "Low density region"이다.

Low density separation: The decision boundary should lie in a low-density region.
클러스터를 나누는 경계는 low-density 영역에 있어야 한다 는 말로 이는 cluster assumption과 동일한 의미로 받아 들일 수 있다.
왜 동일 한 의미로 받아 들일 수 있을까?
  low density separation을 부정해 보자. (엄격한 의미에서 논리 학적인 부정은 아닐 것 같다 더 잘 아시는 분이 있다면 댓글로 이 연결고리를 완성시켜 주시면 좋겠다.)
  결정경계(decision boundary)가 high-density 영역에 놓인다면 결정 경계는 같은 클러스터에 속한 데이터를 서로 다른 class로 분류 하게 된다. 이는 같은 클러스터에 속한 데이터는 같은 클래스를 갖을 것이라는 cluster assumption을 부정 하게 되므로 하나를 부정하면 다른 하나도 부정되기 때문에 같은 말의 다른 표현이라고 할 수 있다.

smoothness assumption 과 cluster assumption의 차이
1. smoothness assumption은 입력 공간에서 인접한 데이터가 대체로 비슷한 출력을 갖는 경향이 있다는 가정이고 cluster assumption은 입력 공간에서 데이터 들이 군집(cluster)을 이루는 경향이 있다는 것이다.
2. smoothness assumption을 이용하면 레이블이 없는 데이터의 출력을 결정하기 위해 이웃하는 레이블이 있는 데이터를 활용할 수 있다.
3. cluster assumption을 이용 하면 레이블이 없는 데이터의 클래스를 결정하기 위해 주변 군집의 정보를 활용할 수 있다.

위 말을 자세히 보면 smoothness assumption은 입력 데이터의 관계와 출력 데이터의 관계가 서로 유사할 것이다 라고 만 말하고 있지 서로 다른 둘을 어떻게 분류 할지에 대한 정보는 담고 있지 않다.
반면 cluster assumption을 서로 다른 둘을 어떻게 분류 할수 있는지에 대한 가정을 담고 있다.

Manifold assumption

The high-dimensional data lie on a low-dimensional manifold

Manifold란 데이터의 내재된 구조를 나타내는 개념이다. 유사하게 데이터가 고차원에 존재할 경우
manifold란 데이터가 실재로 존재하는 저차원 하위 공간(subspace)을 나타 낼 수도 있다.
Manifold learning이란 고차원 데이터를 저차원 manifold 공간으로 맵핑 하는 방법을 의미한다.

manifold assumption은 semi-supervised에서 왜 중요한가?  
high dimensional data의 문제는 연산량 증가, pairwise distance가 유사해 지며 데이터가 자체의 특성이 가려지는 문제 등이다. manifold는 그 개념 자체가 데이터의 내재된 구조, 그 구조를  잘 나타내는 저차원 공간을 나타내기 때문에 manifold에서 density와 distance등을 이용해 데이터 분포를 더 잘/쉽게 표현할 수 있다. 데이터 분포를 더 잘 표현 할 수 있으면 당연히 분포 모델링도 쉬워질 수 있다.

Transduction

transduction을 설명 하기 위해 induction을 먼저 설명해야 할거 같다.
induction이란 귀납적 인것이다. 이는 supervised learing의 기저에 깔린 개념으로 특수한 케이스(학습 데이터 셋)와 그 라벨을 아는 상태에서 입력 데이터와 출력 라벨의 관계를 설명하는 일반적 규칙을 학습하는 것을 목표로 한다. 그 후 학습한 규칙을 unlabeled data에 대입해 label을 추론 한다.

transduction은 학습 과정에서 모든 관측치를 다 사용 한다. 즉 라벨이 있는 관측치든 없는 관측치든 모두 사용 하는 것이다. 모든 관측치를 사용해 공통된 특징, 패턴, 연관관계 등을 학습해 당장 풀고자 하는 목표 문제의 해답만을 찾는 것을 목표로 한다. 즉 일반적인 규칙을 학습하고자 하는 것이 아니다.

transduction 에 대한 개인 적인 의견 
이렇게만 설명되어 있는 글들을 보다 보니 생긴 의문이 그럼 transduction은 너무 한정적인것 아닌가? 였다.
하지만 이는 transduction의 개념일 뿐이다. 어떤 것을 정의 하는 개념과 그것의 특성을 어떻게 사용(application) 할 것인지는 전혀 다른 얘기다. transduction이 unlabeled data를 포함한 사용 할 수 있는 모든 관측치를 이용해 당장 해결하고자하는 문제, 예를 들어 classification,의 최적 답을 찾고자 하는 개념이라면 이 문제를 푸는 과정에서 transduction의 개념을 이용하는 알고리즘은 앞서 말했듯이 labeled data와 unlabeled data 모두를 이용해 그들의 공통적인 성질, 특성등 즉 representation을 추출할 수 있다는 말과도 같을 것이다. 이 특성을 활용 하면 semi-supervised learning에서 transduction의 개념을 차용 할 수 있다.  

(mit press의 semi-supervised learning에서는 transduction과 semi-supervised learning을 동일 한 것으로 보지 않는데 다른 책 또는 블로그에서는 transductive learning = semi-supervised learning이으로 용어를 정의해 설명하기도 해서 서로 다른 책과 블로그에서 설명이 약간 다를 수 있다.)

이번 주제는 Semi supervised learning 이다.

현업에서 일을 하다 보면 무한정 잘 어노테이션 된 데이터를 늘릴 수 없다. 모두가 잘 알듯 이는 비용과 시간이 어마어마 하게 들기 때문이다. 그래서 이를 극복하기 위해 semi-supervised learning을 도입하기로 했고 서베이 할때 읽은 논문들을 하나 씩 정리하고자 한다. 

혹시 semi-superivsed learning 에 대해 기초지식이 전혀 없다면 mit press의 Semi-Supervised Learning 전반부 챕터들이라도 읽어 보길 추천한다. 이보다 더 잘 정리할 수 없을 정도로 잘 정리되어있다. 

그 첫번째가 아래 논문이다. 제목에서 알 수 있듯이 Semi supervised 로 segmantic segmentation 성능을 높이기 위한 접근방식을 도입했다. 

Title: Semi-supervised Semantic Segmentation With Cross-Consistency traning 

link: https://arxiv.org/abs/2003.09005

Contributions

이 논문의 주된 contribution 은 다음 3가지 정도 이다. 

1. consistency를 이용하는 대부분의 method들은 입력 이미지에 서로 다른 변화를 적용하고  서로 다른 변화를 적용한 입력에 대해 네트워크 출력이 일정하도록 학습을 하는데 반해 이 논문은 encoder(또는  backbone)의 출력에 서로 다른 변화를 적용해 main decoder 와 axilary decoder의 입력으로 넣고 decoder의 출력이 일정하도록 학습을 시키는 방법을 제안한다. (axilary decoder 란 학습시에만 쓰이는 decoder로 목적은 encoder의 representation learning 능력을 향상시키는데 있다.)

2. Encoder의 출력인 feature map 에 적용할 다양한 종류의 변화(perturbation) 방법 을 제안하고 실험을 통해 효과를 보여준다.

3. 또한 weakly-labeld data(image level에서의 class 만 가지고 있는 데이터, 이미지넷 과같은 데이터를 생각하면됨)과 서로 다른 도메인의 pixel-level label이 있는 데이터셋을 사용하는 방법도 소개한다.

Method

 저자가 입력 이미지가 아닌 encode 출력인 feature map 에  변화(perturbation)을 적용하기로 한 이유는 다음과 같다. 

저자는 cluster assumption[참조]을 확인 하기 위해 입력 이미지의 특정 위치와 그 이웃 픽셀들 간의 유사성(거리)를 유클리디안 거리로 측정하고 대응 되는 라벨도 유클리디안 거리로 측정했다. 그 입력 이미지에서는 cluster assumption 이 잘 맞지 았다고 한다.  동일 한 실험을 encoder의 출력과 같은 hidden layer의 특정 위치와 그 이웃 위치들 그에 대응되는 라벨에도 대해 실행 했을 때 hidden layer의 출력인 feature space 에서 cluster assumption이 더 잘 들어 맞는 것을 확인했기 때문에 feature map에 perturbation을 적용하기로 결정했다. 

아래 Fig 1 은 위 실험의 결과를 그려 놓은 것이다. (a)는 입력 이미지, (b)는 대응 라벨이다. 

(c) 는 입력 이미지에서 지정된 위치와 그 이웃 위치간의 유클리디안 거리를 측정한 결과(실제 논문에서는 지정된 위치를 center로 하는 20x20 size의 patch 를 기준으로 이미지를 각 셀로 나누고 인접셀의 center 와 유클리디안 거리를 측정했다) (d)는 2048 dimension의 hidden representation space 에서의 지정된 위치와 그 이웃 위치간의 유클리디안 거리를 측정한 결과이다.

(c) 와 (d) 에서 검은 부분은 이웃 위치와 유클리디안 거리가 큰 것을 의미하는데 (d) 에서는 배경 클래스와 전경(강아지, 고양지, 양)등 클래스가 구분되는 곳이 주로 검은색(인접픽셀들과의거리가 먼)으로 나타나는 것이 확인되고 (c) 에서는 그런 경향성이 상대적으로 약하다. cluster assumption에 따르면 low density region에서 결정 경계(decision boundary)가 형성된다고 보기 때문에 (d) 의 실험결과가 cluster assumption을 지지하는 결과라고 할 수 있다.

왜 검은색으로 표기된 영역이 low density region 인가?
혹시 위 글을 읽고 이런 의문이 생겼다면 이렇게 해석을 해보면 된다. low density 영역이란 data point 가 별로 없는 sparse 한 영역을 말한다. 말인 즉 해당 영역에서 특정 data point 까지의 거리가 멀다는 것이다. data point 가 어느 클래스에 속했는지와는 관계 없이 data point들 까지의 평균거리가 먼 위치 임의의 위치가 low density region 인것이다. 그리고 cluster assumption(low density assumption)에서는 이 공간에 결정 경계가 생성된다고 본다.

아래 그림은 논문이 제안하는 네트워크의 구조이다. 이 구조는 하나의 encoder(Shared Encoder, $h$)와 main decoder( $g$ ) 그리고 consistency를 강제 하기 위한 auxiliary decoder($g^{l}_{a}, ..., g^{K}_{a}$) 가 존재한다. auxiliary decoder 는 학습시에만 사용 되고 실제 inference time 에는 사용되지 않는다. 

total loss는 아래와 같다.

$$ L = L_{s} + \omega_{u}L_{u} $$

 $L_{s}$ 는 label 이 존재하는 데이터로 구한 cross entropy loss , 즉 supervised loss term이고

$L_{u}$ 는 unlabeled data를 이용해 구한 consistency loss 이다.  $\omega_{u}$는 $L{s}$ 와의 밸런스를 맞추기 위한 텀으로 learning rate 처럼 학습 중 규칙에 따라 조절 된다. 

$L_{s}$ 는 label 이 존재하는 데이터로 부터 구한 loss 이다. Fig 2 의 model architecture 에서 labeled example $X^{l}$ 이 입력으로 사용 될때 main decoder( $g$ )의 출력 $\hat{y}^{l}$과 label $y$를 이용해 cross entropy loss 를 구한 것이다. 논문에서는 이를 아래 식으로 표현했다.여기서 $f$ 는 encoder와 main decoder 를 포함한 network을 의미 하고 $H$ 는 cross entropy loss 이다. 

이제 Unlabeled data를 어떻게 이용하는지 보자. 여기가 중요 포인트 이다. 

Shared Encoder( $h$)의 출력을 $z_{i} = h(X^{u}_{i})$ 라 하자.  이 논문의 contribution 1 과 같이 저자들은 이 $z_{i}$ 에 작은 변화(pertubation) 을 적용해

각 auxilary decoder( $g^{l}_{a}, ..., g^{K}_{a}$) 입력으로 들어갈 $K$ 개의 서로 다른 $\tilde{z}^{a}_{i}, ... , \tilde{z}^{K}_{i}$ 를 생성한다.

이렇게 생성된 $\tilde{z}$ 들은 각 auxiliary decoder 의 입력으로 들어가게 되고 대응 되는 출력 $\hat{y}^{(l)}_{a}, .., \hat{y}^{(K)}_{a}$ 을 생성한다.  auxiliary decoder와는 다르게 main decoder( $g$) 에는 변화가 적용되지 않은 순수한 encoder output 인 $z_{i}$ 가 입력으로 들어가 출력 $\hat{y}^{u}$ 를 생성한다.

auxiliary decoder의 출력 $\hat{y}^{(l)}_{a}, .., \hat{y}^{(K)}_{a}$은 main decoder의 출력을 target 으로 mean square error 를 이용해 학습 한다.  즉 auxiliary decoder 의 출력이 main decoder의 출력과 같아지는 것을 목표로 학습을 하는 것이고 이는 feature의 작은 변화에도 모델 안정적인 추론 성능을 갖도록 학습하는 것이다.

또한 main decoder의 출력은 target 즉 ground truth 로 활용 되므로 unlabeled data를 이용해 학습을 할때 main decoder의 weight 들은 학습 되지 않는다.

이를 수식으로 정리하면 다음과 같다.

이렇게 학습 하면 결과적으로  encoder 의 representation 능력을 강화 하는 방식으로 학습이 진행된다.

Perturbation

이제 shared encoder의 출력인 $z_{i}$에 어떤 변화(perturbation)을 적용해 auxiliary decoder의 입력으로 활용했는지 알아 보자. 글만 보면 정확히 파악하기 힘들수 있으니 각 perturbation을 구현한 저자의 코드를 같이 정리한다.

 feature based perturbation:

이 타입의 perturbation 기법은 feature 에 noise를 더하거나 drop out 하는 것을 말한다.

• F-Noise: feature 와 같은 dimension 을 가지는 noise tensor를 uniform distribution 으로 부터 추출하고 feature 더하는 방식이다.

class FeatureNoiseDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes, uniform_range=0.3):
        super(FeatureNoiseDecoder, self).__init__()
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)
        self.uni_dist = Uniform(-uniform_range, uniform_range)

    def feature_based_noise(self, x):
    	#바로 아래 라인이 uniform distribution 으로 부터 noise vector 를 추출하는 라인이다. 
        noise_vector = self.uni_dist.sample(x.shape[1:]).to(x.device).unsqueeze(0) 
        x_noise = x.mul(noise_vector) + x #feature 에 노이즈를 적용한다. 
        return x_noise

    def forward(self, x, _):
        x = self.feature_based_noise(x)
        x = self.upsample(x)
        return

• F-dropout: feature map($z$)을 채널 축으로 summation 하고 normalization 해 $z^\prime$ 을 생성하고 0.6~0.9 사이의 random 값 $\gamma$ 를 threshold 로 정해 $\gamma$ 보다 작은 위치의 feature 를 0으로 만드는 방식이다. $M_{drop} = { z^\prime < \gamma}_{1}$  로 0으로 만들 위치를 mask 로 만들고 $\tilde{z} = z x M_{drop} $ 과 같이 적용한다.

class FeatureDropDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes):
        super(FeatureDropDecoder, self).__init__()
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def feature_dropout(self, x):
        attention = torch.mean(x, dim=1, keepdim=True)
        max_val, _ = torch.max(attention.view(x.size(0), -1), dim=1, keepdim=True)
        threshold = max_val * np.random.uniform(0.7, 0.9) # 논문은 0.6~0.9 사이로 적었는데 구현은 0.7~0.9 사이이다.
        threshold = threshold.view(x.size(0), 1, 1, 1).expand_as(attention)
        drop_mask = (attention < threshold).float()
        return x.mul(drop_mask)

    def forward(self, x, _):
        x = self.feature_dropout(x)
        x = self.upsample(x)
        return x

Prediction based perturbation:

이 방식은 main decoder의 출력을 $\hat{y} = g(z)$ 이용해  object 가 차지하는 영역의 pixel을 변화시키거나 object 가 차지 하지 않는 영역을 변화시키기 위한 기법이다. object 내의 영역에 작은 변화를 일으키는 이유는 데이터셋에 존재하는 object의 특정 부위에 집중해 하거나, 특정 view angle 에서 바라본 object의 모습 등에 overfitting 되는 것을 피하기 위한 것으로 볼수 있다. object 이외의 영역을 변화시키는 mask 를 생성하는 이유는  학습 데이터셋에  존재하는 context information 로 인한 bias 를 줄이기 위한것으로 해석 할 수 있다. 

context information 이란 
"Context is a statistical property of the world we live in and provides critical information to help us solve perceptual inference tasks faster and more accurately" 이라고 할 수 있다. 우리가 사물을 인지 하는데 이용하는 정보로 object detection task 에서는 특정 object 가 있을 법한 "주위 환경 정보"를 임의의 object 클래스를 정하는데 활용 한다거나 학습 데이터 셋에 존재하는 object 들 간의 관계를 학습하는 것으로 볼수 있다. 예를 들으 밀림이라는 background에 호랑이가 있는 이미지가 학습데이터 셋에 많고, 집안 벽에 걸려 있는 호랑이 사진 또는 그림이 있을 경우 "집안의 가구와 같이 있는 호랑이 이미지"가 주어졌을때 호랑이 자체가 아닌 호랑이와 주변 가구 사이의 관계를 이용해  "호랑이 사진/그림" 으로 prediction 하게 된다던지 하는 것이다. 

• guided masking: main decoder의 출력을 이용해 object 가 차지하는 영역에만 perturbation 을 적용하거나 object 이외의 context 에만 perturbation 을 적용하는 방식이다. 아래 코드에서 pred 는 main decoder의 출력이다. 

def guided_masking(x, output, upscale, resize, return_msk_context=True):
    if len(output.shape) == 3: 
        masks_context = (output > 0).float().unsqueeze(1)
    else: 
        masks_context = (output.argmax(1) > 0).float().unsqueeze(1)
    
    masks_context = F.interpolate(masks_context, size=resize, mode='nearest')

    x_masked_context = masks_context * x
    if return_msk_context:
        return x_masked_context

    masks_objects = (1 - masks_context)
    x_masked_objects = masks_objects * x
    return x_masked_objects


class ContextMaskingDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes):
        super(ContextMaskingDecoder, self).__init__()
        self.upscale = upscale
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def forward(self, x, pred=None):
        # pred 는 main decoder의 출력결과이다. 
        x_masked_context = guided_masking(x, pred, resize=(x.size(2), x.size(3)),
                                          upscale=self.upscale, return_msk_context=True)
        x_masked_context = self.upsample(x_masked_context)
        return x_masked_context


class ObjectMaskingDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes):
        super(ObjectMaskingDecoder, self).__init__()
        self.upscale = upscale
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def forward(self, x, pred=None):
    	# pred 는 main decoder의 출력결과이다. 
        x_masked_obj = guided_masking(x, pred, resize=(x.size(2), x.size(3)),
                                      upscale=self.upscale, return_msk_context=False)
        x_masked_obj = self.upsample(x_masked_obj)

        return x_masked_obj

• guided cutout: object 의 특정 부분에 의존적으로 추정하는 것을 방지하기 위해 object 영역내 임의의 위치를 0으로 만드는 perturbation을 적용한다.  segmenation map으로 부터 object의 contour를 찾고 이를 이용해 bounding box 를 만든다 그리고 bouding box 내의 임의 사격형 영역을 0으로 만든다.

def guided_cutout(output, upscale, resize, erase=0.4, use_dropout=False):
    if len(output.shape) == 3:
        masks = (output > 0).float()
    else:
        masks = (output.argmax(1) > 0).float()

    if use_dropout:
        p_drop = random.randint(3, 6)/10
        maskdroped = (F.dropout(masks, p_drop) > 0).float()
        maskdroped = maskdroped + (1 - masks)
        maskdroped.unsqueeze_(0)
        maskdroped = F.interpolate(maskdroped, size=resize, mode='nearest')

    masks_np = []
    for mask in masks:
        mask_np = np.uint8(mask.cpu().numpy())
        mask_ones = np.ones_like(mask_np)
        try: # Version 3.x
            _, contours, _ = cv2.findContours(mask_np, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
        except: # Version 4.x
            contours, _ = cv2.findContours(mask_np, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

        polys = [c.reshape(c.shape[0], c.shape[-1]) for c in contours if c.shape[0] > 50]
        for poly in polys:
            min_w, max_w = poly[:, 0].min(), poly[:, 0].max()
            min_h, max_h = poly[:, 1].min(), poly[:, 1].max()
            bb_w, bb_h = max_w-min_w, max_h-min_h
            rnd_start_w = random.randint(0, int(bb_w*(1-erase)))
            rnd_start_h = random.randint(0, int(bb_h*(1-erase)))
            h_start, h_end = min_h+rnd_start_h, min_h+rnd_start_h+int(bb_h*erase)
            w_start, w_end = min_w+rnd_start_w, min_w+rnd_start_w+int(bb_w*erase)
            mask_ones[h_start:h_end, w_start:w_end] = 0
        masks_np.append(mask_ones)
    masks_np = np.stack(masks_np)

    maskcut = torch.from_numpy(masks_np).float().unsqueeze_(1)
    maskcut = F.interpolate(maskcut, size=resize, mode='nearest')

    if use_dropout:
        return maskcut.to(output.device), maskdroped.to(output.device)
    return maskcut.to(output.device)


class CutOutDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes, drop_rate=0.3, spatial_dropout=True, erase=0.4):
        super(CutOutDecoder, self).__init__()
        self.erase = erase
        self.upscale = upscale 
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def forward(self, x, pred=None):
        maskcut = guided_cutout(pred, upscale=self.upscale, erase=self.erase, resize=(x.size(2), x.size(3)))
        x = x * maskcut
        x = self.upsample(x)
        return x

• Intermediate VAT: inference 를 가장 혼란 스럽게 만들 수 있는 변화를 feature 에 적용 하는 방식으로 virtual adverserial training을 응용했다. VAT에서는 noise 를 샘플링 한 후에, 해당 noise 를 더한 값과 기존의 값의 차이(KL-div)의 gradient 를 이용해 noise 를 생성한다.(todo: 부분은 따로 정리 할 것.)

def get_r_adv(x, decoder, it=1, xi=1e-1, eps=10.0):
    """
    Virtual Adversarial Training
    https://arxiv.org/abs/1704.03976
    """
    x_detached = x.detach()
    with torch.no_grad():
        pred = F.softmax(decoder(x_detached), dim=1)

    d = torch.rand(x.shape).sub(0.5).to(x.device)
    d = _l2_normalize(d)

    for _ in range(it):
        d.requires_grad_()
        pred_hat = decoder(x_detached + xi * d)
        logp_hat = F.log_softmax(pred_hat, dim=1)
        adv_distance = F.kl_div(logp_hat, pred, reduction='batchmean')
        adv_distance.backward()
        d = _l2_normalize(d.grad)
        decoder.zero_grad()

    r_adv = d * eps
    return r_adv


class VATDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes, xi=1e-1, eps=10.0, iterations=1):
        super(VATDecoder, self).__init__()
        self.xi = xi
        self.eps = eps
        self.it = iterations
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def forward(self, x, _):
        r_adv = get_r_adv(x, self.upsample, self.it, self.xi, self.eps)
        x = self.upsample(x + r_adv)
        return x

random perturbations: 

가장 단순한 형태로 drop out을 이용한다. 

class DropOutDecoder(nn.Module):
    def __init__(self, upscale, conv_in_ch, num_classes, drop_rate=0.3, spatial_dropout=True):
        super(DropOutDecoder, self).__init__()
        self.dropout = nn.Dropout2d(p=drop_rate) if spatial_dropout else nn.Dropout(drop_rate)
        self.upsample = upsample(conv_in_ch, num_classes, upscale=upscale)

    def forward(self, x, _):
        x = self.upsample(self.dropout(x))
        return x

Avoiding overfitting

라벨이 있는 데이터가 라벨이 없는 데이터 보다 적은 상황에서 각 iteration 마다 동일한 크기의 label, unlabeled 데이터를 추출해 학습하므로 label 이 있는 데이터가 실제 학습에 중복되어 사용되기 때문에 overfitting 이 발생할 수 있다. 이를 방지 하기 위해 bootstrapped-CE(ab-CE, CE=cross entropy)를 사용했다. 

$f(x^(l)_{i})$ 은 라벨이 있는 데이터 $x$ 에 대한 모델의 출력으로 모델이 $x^(l)_{i}$가 특정 클래스에 속할 활률을 $\eta$ 로 추측하는 pixel들만 supervised loss 계산에 사용 하겠다는 의미이다. 즉 모델이 이미 $\eta$ 의 확신을 가지고 추론한 pixel 은 더 이상 학습에 이용하지 않음으로서 overfitting 을 방지하겠다는 전략이다. 

결론

학습과 관련된 정확한 정보는 논문을 참조하기로 하고 결론을 보자.(wealky-labeled data, joint leraning of difference domain data 에 대한 것은 결론 이후에 정리한다.)

Fig 3은 camvid 데이터 셋에서 라벨이 있는 이미지를 각각 20, 50, 100장 사용해 unlabeled data 와 학께 학습한 결과이고 Fig4는 PASCAL VOC에서 1000장의 라벨이 있는 이미지와 unlabeled data 데이터를 이용해 학습한 결과이다. 

Fig 3에서 보면 당연하게도 label 이 있는 데이터의 사용량이 증가 할 수록 baseline  miou가 20, 30, 38.x 와 같이 증가하는 경향성을 갖는다는 것을 알수 있다. x측은 특정 타입의 auxiliary decoder를 몇개 사용 했는지를 나타내는데 K =2 이라면 CCT F-dop의 경우 F-drop type의 auxiliary decoder를 2개 사용, K=4 이면 해당 타입 decoder 를 4개 사용 했다는 의미이다.  CCT full은 위에 소개된 perturbation을 적용한 decoder 를 모두 사용 한 경우 이고 이 경우 K=2라면 F-noise decoder 2개, F-drop decoder 2개, gropout decoder 2개, G-cutout(guided cutout) decoder 2개, VAT(virtual adverserial training) decoder 2개, object mask decoder 2개, context mask decoder 2개 등 총 number of perturbation x K 개의 decoder 를 사용해 학습 했다고 해석 하면 된다. CCT full +abCE 는 모든 종류의 perturbation을 사용하고 bootstrapped -CE를 함께 사용한 결과이다.

camvid dataset 실험결과의 경우 모든 종류의 perturbation을 다 사용하고 각 perturbation type의 decoder 개수가 많아 질수록 성능이 좋아진다. PASCAL의 경우 모든 perturbation type을 사용하고 bootstrapped -CE 까지 사용 할 경우 K=2 일 때 성능이 가장 우수 했다. 

전반적인 결과는 논문에서 제안한 feature perturbation 방식과 consistency loss 를 사용 할 경우 라벨이 있는 데이만 사용 할때 보다 더 좋은 성능을 낼수 있는 것으보인다. 

Fig 5는 다른 state-of-the-art 방법들과 PASCAL VOC 데이터를 이용해 학습한 결과를 비교한 표인다. 이 논문에서 제안한 CCT 방식이 성능이 가장 좋았다는 결과이다. 

Use weak-labels

이 논문에서는 weak-label data 를 이용하는 방법에 대해서도 다루고 있다. 간단하게만 살펴 보자. 

weak label 은 이미지 레벨에서 어떤 object 가 있는지에 대한 정보가 있는 상태로 정의 된다. 이미지넷 데이터 셋을 생각해보자. 이를 이용해서 특정 object에 대한 부가 적인 표현 정보(representation)을 encoder가 학습 할 수 있게 만드는게 목표 이다. 

이를 위해 사전학습 된 encoder 와 classification branch를 이용한다. classification branch를 이용해 class activation map을 생성하고 이 map 에서 activation score 가 특정 threshold $\theta_{bg}$(논문에서는 0.05) 미만 이면 background class , 특정 threshold $\theta_{fg}$ (논문에서는 0.3) 초과면 weak-label 에 해당하는 foreground class 로 간주해 pseudo ground truth map($y_{p}$) 을 생성하고 이 pseudo ground truth map 에 dense CRF 를 적용해 한번더 정재 한 후 이를 auxiliary decoder  학습에 사용한다. 

$L_{w}$가 weak label data를 이용한 weakly supervised loss 이고 $g^{k}_{a}$는 auxiliary decoder, $z_{i}$는 encoder output, $y_{p}$는 class activation map 기반의 pseudo gt 이다. 

Cross-consistency traning on mutiple domains

이번엔 다른 도메인의 label-unlabeled data set 을 이용해 학습 하는 방법이다. 굉장히 쉽고 직관적인 아이디어 이다. 

사실 다음 그림으로 이미 설명이 끝난다. 

서로 다른 도메인의 data set $D^{(1)}, D^{(2)}$ 를 이용하는데 $D^{(*)} = { D^{(*)}_{l} \cup D^{(*)}_{u} }$  로 $ D^{(*)}_{l} $ 는 도메인 *에 속한 라벨이 있는 데이터 $ D^{(*)}_{u} $ 은 도메인 *에 속한 라벨이 없는 데이터 이다. 

이 두 도메인 데이터를 이용해 학습하는데 encoder $h$ 는 공유 하고 각 도메인의 main decoder과 auxiliary decoder를 따로 따로 사용해 학습을 진행한다. 이렇게 하면 두 도메인의 데이터를 모두 이용해 encoder 가 특정 object의 representation 을 학습하는데 도움이 된다고 한다. 

-끝-