이번에 정리할 논문은 MobileViT로 transformer와 convolution을 조합해 더 좋은 feature를 학습할 수 있음을 보인 논문이다.

제목: MobileViT
link: https://arxiv.org/pdf/2110.02178.pdf

인트로 덕션 요약:

self-attention-based 모델은 컨볼루션 네트웍의 대안이다.
ViT 계열의 트랜드는 모델 파라미터를 늘려서 성능을 끌어 올리는 방식인데 이는 모델 사이즈를 키우고 latency를 증가시킨다. 따라서 edge device 같은 자원이 제한적인 환경에서 이는 문제가 된다.

mobile device의 자원 제약을 충족할 정도로 Vit 모델 사이즈가 줄어 들 수 있지만 DeIT(Touvron et al., 2021a) 의 경우에서 보이듯 light-weight CNN(MobileNetV3)보다 3% 낮은 성능을 보일 정도로 성능하락이 심하다.

Vit 계열의 문제점은
1. 모델이 무겁다. ex) ViT-B/16 vs mobileNetV3: 86 vs 7.5 million parameters
2. 최적화 하기 어렵다(Xiao et al., 2021 )
3. 오버 피팅을 방지 하기 위해 광범위한 Data augmentation 과 L2 regularization 이 필요하다. (Touvron et al., 2021 a; wang et al., 2021)
4. dense prediction task ex) segmentation,과 같은 down-stream task 를 위해 무거운 decoder가 필요하다. (ex. Vit-base 세그멘테이션 네트웍(Ranftl et a. 2021.,) 은 345 million parameters를 사용해 CNN계역의 DeepLabv3(59 million parameters)와 비슷한 성능을 얻었다.)

ViT 가 비교적 많은 파라미터를 필요로 하는 것은 CNN 계열이 선천적으로 지니고 있는 image-specific inductive bias가 부족하기 때문으로 보인다. (Xiao et al., 2021)

강인한 고성능 Vit 모델 개발을 위해 convolution과 transformers의 결합이 주목받고 있다. (xiao et al., 2021, d'Ascoli et al., 2021; Chen et al., 2021b). 그러나 이런 모델은 여전히 무겁고 data augmentation 에 예민하다.
증거로, Cutmix와 DeIT-style data augmentation 을 제거하면 Heo et al(2021)은 imageNet accuracy가 78.1% 에서 72.4% 로 감소한다.

이러한 이유로 CNN과 transformer의 강점을 조합해 mobile vision task를 위한 ViT 모델을 만드는 것은 여전히 숙제로 남아있다.(본인들 연구 정당성을 이렇게 정성들여 조목조목 주장할 수 있는 건 정말 큰 능력인것 같다.)

이 논문에서 저자는 light-weight, general-purpose, low-latency이 3가지 관점에 초점을 맞춰 mobilevit라는 모델을 제안한다.

여기서 low-latency와 관련해 FLOPs라는 지표가 적절하지 않다고 언급하는데 이유는 다음과 같다.

FLOPs는 아래와 같은 latency에 영향을 미치는 요소들을 고려하고 있지 않다.
1. 메모리 엑세스
2. 병렬성 정도
3. 플랫폼 특성
그 증거로 PiT는 DeIT 에 비해 1/3배의 FLOPs 를 가지고 있으나 iPhone-12에서 비슷 한 latency를 보여준다.
(10.99ms vs 10.56ms)
따라서 이 논문은 FLOPs 측면에서의 최적화를 목표로 하지 않는다. (즉, FLOPs는 상대적으로 큰 편이다...)

정리: MobileVit는 CNNs의 장점인 spatial inductive biases 와 less sensitivity to data augmentation 과
ViT의 장점인 input-adaptive weighting and global processing을 잘 조화했다.(가 주장하는 바이다.)

특히 MobileVit block를 제안하는데 이 블럭은 local 과 global information 모두를 tensor 효율적으로 encode 한다. (한글로 풀어 쓰고 싶은데 표현하기 정말 난해 하다...)
Convolution을 사용/사용 하지 않는 ViT 계열과는 다르게, mobileVit는 global representation을 학습하는데 다른 관점을 지니고 있다.
standard 컨볼루션은 3개 연산으로 이루어 진다. unfolding, local processing, folding.
MobileVit Block은 local processing을 transfomer를 이용한 global processing으로 치환해서 CNN과 ViT의 특성을 가진다. 그로인해 적은 수의 파라미터와 간단한 학습 레시피(data augmentation이 ViT에 비해 간단함을 의미) 더 좋은 feature를 배운다.

결과적으로 MobileViT는 5~6million의 파라미터 수로 mobileNetV3보다 3.2% 더 높은 Top-1 accuracy를 ImageNet-1k dataset에서 보여 준다.

기존 모델들의 한계:

light-weight cnn:

공간적으로 local information에 의존한다. Convolution 필터 자체가 인접 픽셀들간의 관계로 부터 representation을 학습하니 당연하다.
다만 layer가 깊어 질수록 receptive field가 커짐에도 불구하고 이렇게 표현한 걸 보면 상대적으로 local 하다는 표현인것 같다.

Vision transformer:

많은 파라미터를 사용한다.
데이터가 크지 않으면 오버피팅 문제가 있다.
extensive data augmentation 이 필요하다.
convolution을 이용하는 ViT 모델들도 있지만 여전히 heavy weight이고 light-weight CNN 모델들 수준으로 파라미터 수를 줄이면 CNN 계열 보다 성능이 떨어지는 문제를 한계로 지적했다.

ViT 계열은 image-specific spacial inductive bias가 부족 하기 때문에 더 많은 파라미터와 data augmentation이 필요하다고 언급하는데 convolution을 ViT에서 이용 함으로서 이 부족한 inductive bias를 ViT 모델에 이식할 수 있다고 한다.

논문에서 언급된 여러 모델들이 convolution을 ViT 모델에 서로 다른 방식으로 이용해 CNN과 ViT의 장점을 이용해 강건하고 고성능의 ViT 만들었다고 한다. 하지만 여전히 남은 문제는 "convolution과 ViT를 어떻게 조합해야 둘의 강점을 잘 이용 할수 있는가?" 라는 점이다.

위와 같은 문제를 가지고 있는 기존 방식에 비해 MobileVit의 강점은 :

1. Better performance(주어진 파라미터 한계에서 light-weight CNN 보다 높은 성능을 보임)
2. Generalization capability: 다름 ViT variant 모델들 모다 generalization capability가 좋음
3. Robust: Data augmentation과 L2 regularization에 덜 민감함

MobileViT block:

이 논문의 핵심은 MobileViTBLock을 통해 적은 수의 파라미터로 local 과 global information을 modeling 하는 것이다.

Fig 1 의 녹색 영역은 MobileViTBlock의 연산을 도식화한 것이다.
MobileVitBlock에서 local spacial information ( Fig 1 녹색 영역의 Local representations 로 표시된 부분)은
$n \times n$ convolution을 이용해 획득하고 point-wise convolution을 이용해 인풋 텐서 채널의 선형 조합으로 고차원 정보를 생성한다. --------------------------------------------------------------------------------------(1)

global information은 multihead attention을 이용해 학습하게 된다.

input을 $X_L$이라 할때 $X_L$을 서로 오버랩 되지 않는 patch $X_U = R^{P \times N \times d}$ 로 나타낸다.
$P = w \times h$ 로 h,w는 패치의 가로,세로 크기 이고, $N=\frac{HW}{P}$은 input tensor내에 존재하는 패치의 수이다.

transformer가 local spatial information과 inter_patch 정보를 모두 모델링 하기 위해서는 h<=n, w<=n 을 반드시 만족해야 한다. 즉 non-overlap 패치의 크기는 convolution kernel의 크기보다 반드시 같거나 작아야 한다.

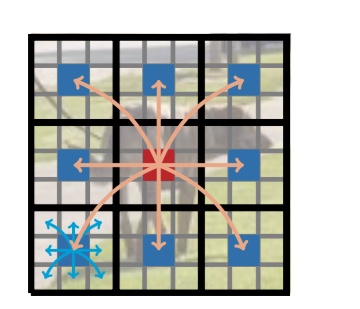
아래 그림 Fig 2는 MobileViTBlock 이 왜 local 과 global representation을 모두 학습 할 수 있는 지 보여준다.
검은 색 굵은 선으로 분리된 각 영역은 오버랩되지 않은 patch이고, 각 patch 내 회색 선으로 분리된 공간은 patch에 속하는 pixel 이라 보면 된다. 왼쪽 하단의 patch를 보면 파란색 화살표가 파란색으로 표시된 pixel 주변의 정보를 취학하는 것을 표현 했는데 이는 $ n \times n$ convolution을 통해 이루어 진다. 아래 그림의 정가운데 위치한 patch 내에 붉은 색으로 표시된 pixel은 다른 patch의 자신과 동일 한 위치의 pixel들의 정보를 취합 하는데 이과정이 multi-head attention을 통해 이루어 진다.

이를 좀더 수식 적으로 표현 하면 $p = {1,...,P}$ 라 할때 패치간의 관계는 모델은 다음과 같이 표현 할 수 있다.
$$ X_{G}(p)=Transformer(X_{U}(p)), 1<=p<=P$$
ViT와 다르게, 위와 같이 모델링 되는 MobileVit는 패치간의 순서나 pixel의 공간 정보도 잃지 않기 때문에 MobileVitBlock의 입력 $X_{L}$의 각 픽셀 위치에 해당하는 local, global information이 축약된 정보를 입력 모양에 맞게 $X_{F}=R^{H \times W \times d}$로 복원가능 하다.
그 후 $X_{F}$는 point-wise-convolution을 이용해 저차원으로 projection 되고 mobileVitBlock의 입력 X와 concat된 후 $n \times n$ convolution을 이용해 feature를 혼합한다.

$X_{U}$은 $n \times n$ convolution으로 local information을 학습하고 $X_{G}$는 패치간의 정보를 취합하기 떄문에 $X_{G}$의 각 픽셀은 결국 입력 X의 모든 정보를 취합한다고 볼수 있다.
(코드 상으로 보면 X_G의 임의의 패치 p에 속한 임의의 pixel i(hi,wi)는 X_G의 오버랩 되지 않는 p가 아닌 다른 패치들의 q에 속한 pixel j(hi,wi)위치와 attention이 계산되므로 엄밀히 말하면 모든 픽셀에 대한 정보를 취합하는 것이 아니라 다른 패치 내의 동일한 위치에 있는 pixel의 정보만 취합한다. 따라서 입력 X의 모든 픽셀에 대한 정보를 X_G가 취합 하게 하려면 nxn convolution의 커널 사이즈 n와 , 패치 사이즈 h,w를 신중하게 디자인 해야 한다. )

코드로 보면 더 직관 적이니 아래 코드를 보자.
각 라인 옆에 위 설명의 $X_{L}$, $X_{U}$, $X_{G}$에 해당 하는 값을 표기해 두었다.

class MobileViTBlock(nn.Module):
    def __init__(self, dim, depth, channel, kernel_size, patch_size, mlp_dim, dropout=0.):
        super().__init__()
        self.ph, self.pw = patch_size

        self.conv1 = conv_nxn_bn(channel, channel, kernel_size)
        self.conv2 = conv_1x1_bn(channel, dim)

        self.transformer = Transformer(dim, depth, 4, 8, mlp_dim, dropout)

        self.conv3 = conv_1x1_bn(dim, channel)
        self.conv4 = conv_nxn_bn(2 * channel, channel, kernel_size)
    
    def forward(self, x):
        y = x.clone()

        # Local representations
        x = self.conv1(x)
        x = self.conv2(x) # 여기서 x = X_L 이다.
        
        # Global representations
        _, _, h, w = x.shape
        x = rearrange(x, 'b d (h ph) (w pw) -> b (ph pw) (h w) d', ph=self.ph, pw=self.pw)
        x = self.transformer(x) # 파라미터 x = X_U 이고 output x = X_G이다. 
        x = rearrange(x, 'b (ph pw) (h w) d -> b d (h ph) (w pw)', h=h//self.ph, w=w//self.pw, ph=self.ph, pw=self.pw)
		# 바로 윗 라인의 reshaped 된 x = X_F에 해당 된다. 
        
        # Fusion
        x = self.conv3(x)
        x = torch.cat((x, y), 1)
        x = self.conv4(x)
        return

relationship to convoltuions:

컨볼루션은 아래와 같은 3개 연산의 스택으로 볼 수 있다. Fig 1 의 녹색 영역을 참고해서 보면 좀더 쉽게 이해 할 수 있다.
1. unfold
2. matrix multiplication
3. fold
본 논문에서 제시한 mobileVitBlock는 아래와 같은 3단계 연산을 한다는 측면에서 transformer를 convolution 처럼 본다고 볼수 있다.
1. 입력 $X_{L} \in \in R^{H \times W \times d}$을 non-overlaping patch $X_{U} \in R^{P \times N \times d}$로 unfolding 하고
-> convolution의 unfolding에해당
2. transformer layer를 통해 global representation을 배우고
-> convolution의 matrixmultiplication에 해당
3. transformer의 output인 $X_{G} \in R^{P \times N \times d}가 patch order와 pixel order를 잃지 않았기 때문에 $X_{F} \in R^{H \times W \times d}$로 복원
-> convolution의 folding에 해당

개인 적으로 transformer를 convolution 처럼 볼수 있다는 해석 보다 non-overlaping 패치 간의 feature relation을 모델링 하기 위해 swin transformer 가 axis roll 을 사용 한것 보다 본 논문에서 convolution과 transformer 블럭을 사용해서 local, global feature representation을 학습하는 전략이 더 간단하고 효과적으로 보인다.

light-weight:

기존 convolution + transformer 사용 네트워크가 heavy했기 때문에 같은 레이어의 조합을 사용하는 MobileViT가 왜 light-weight 이 가능 한지 의문이 들 수 있다. 저자는 그 이유를 다음과 같이 말한다.
기존의 convolution과 transformer를 사용하던 네트워크는 spatial information을 latent로 바꾼다.
이게 무슨 말인고 하니 아래 그림 Fig 3을 보자.

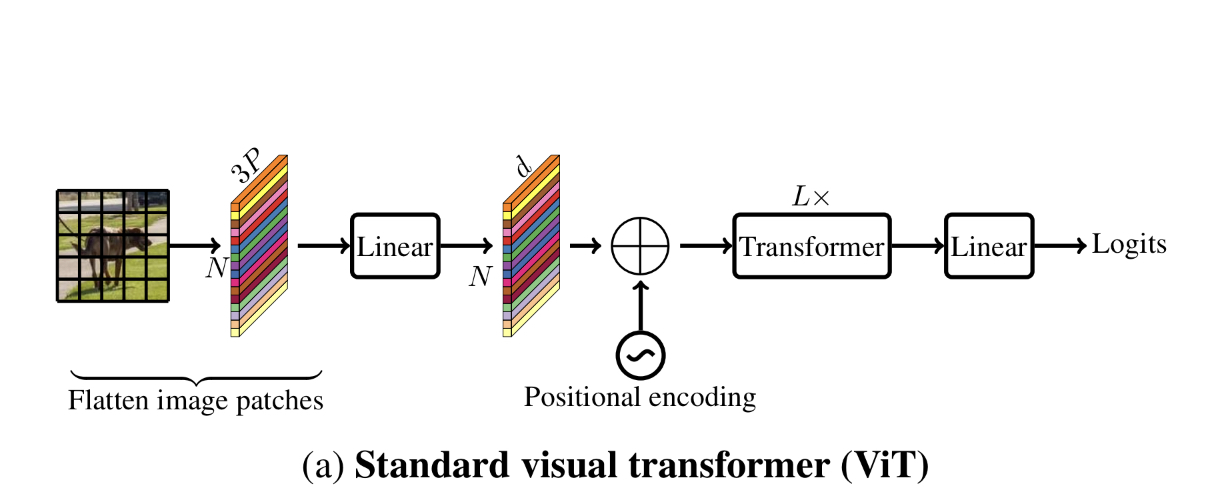
transformer 적용시 인접 픽셀을 채널축으로 stack 하고 픽셀 값들을 linear 연산을 이용해 latent로 보내는 embeding 연산이 image-specific inductive bias를 잃게 하는데 반해
MobileViT는 convolution과 transformer를 convolution의 특징을 살리면서 global representation을 배울 수 있는 방향으로 사용하기 때문에 light weight이 가능 하다는 입장이다.

Multi-head self-attention의 계산 복잡도를 비교해 보면
MobileViT: $O(N^{2}Pd)$
ViT: O(N^{2}d)
로 MobileViT가 더 비효율 적으로 보인다. 하지만 실제로는 MobileViT가 DeIT보다 약 1/2배의 FLOPs 를 가지고 ImageNet-1K 에서 1.8%더 높은 accuracy를 보였다.
이럴수 있는 이유 역시 convolution과 transformer를 서로의 장점을 살리는 방식으로 조합했기 때문에 가능했다는 것이 논문의 주장이고 결과가 좋으니 맞는 말로 보인다.

Multi-Scale Sampler For Training Efficiency:

MobileViT를 학습 시키기 위해 multi scale training 전략을 사용 했는데 기존 방식과 크게 두가지 다른점 이 있다.
이 두가지 다른점은 기존 multi-scale training 방식의 다음과 같은 단점을 보완한 것이다.

1. ViT 계열 네트워크는 multi scale training을 위해 각 scale 별로 네트워크를 fine tuning 하는 방식을 취한다. 왜냐면 ViT의 positional embedding이 입력 이미지 사이즈에 따라 interpolation 되어야 하고 네트워크의 성능이 이 positional embedding의 interpolation 방식(?) 에 영향을 받기 때문이다.

2. CNN 계열 네트워크들은 학습 중 미리 정해진 입력 이미지의 사이즈 $set S=((H_{0},W_{0}), ..., (H_{n}, W_{n}))$중 하나를 정해진 iteration 마다 선택해 학습에 활용하는데 이렇게 하면 batch size가 가장 큰 입력 이미지 사이즈에 의해 고정적으로 결정되기 때문에 작은 입력 이미지 사이즈를 이용해 학습할 때는 GPU 사용율이 떨어질수 밖에 없다. Fig 4 (a) 의 Multi-scale sampler를 보면 여기서 지적한 문제를 도식화 했다. Standard sampler에 비해 gpu memory utilization이 떨어지는 것을 표현했다.

위 두 가지 문제를 해결하는 multi scale sampling scheme은 다음과 같다.
1. MobileViT의 경우 positional embedding이 필요 없기 때문에 파인튜닝 방식으로 multi scale training scheme을 사용 할 필요 없이 CNN 계열 네트워크 처럼 학습 중 기 정해진 방식으로 multi scale training을 사용 한다.

2. 기존 방식에 존재 하던 비효율적 batch size 선택을 개선하는 방법으로 가장 큰 입력 이미지 사이즈를 $(H_{n}, W_{n})$, 이때의 batch size 를 b 라 할때
i-th iteration의 배치 사이즈 $b_{t}$ 는 $b_{t} = \frac{H_{n} * W_{n} * b}{H_{i}*W_{i}} 를 사용하게 함으로써 gpu utilization 문제를 해결한다.

결과적으로 위와 같은 2가지 보완점을 적용한 multi-scale sampler를 사용 할 경우 Fig 4 (b) 같이 standard sampler 보다 학습 효율이 좋아지는 것을 볼 수 있다.

Experimental result:

Dataset: image classification on The ImageNet-1k Dataset
implementation details:
MobileVit를 from scratch로 imageNet-1k 에 학습 시킴, 1.28 million training image, 50,000 validation image.
GPU: 8 NVIDIA GPU 사용
framework: pytorch
batch size: 1024
epoch: 300
기타 :
label smoothing cross-entropy(smoothing=0.1),
multi-scale sampler(S={(160,160), (192,192), (256,256), (288,288), (320, 320)},
L2 waeight dacay( 0.01),
lr scheduler: consine annealing (0.0002~0.002 warm start)

CNN모델들과 비교 :

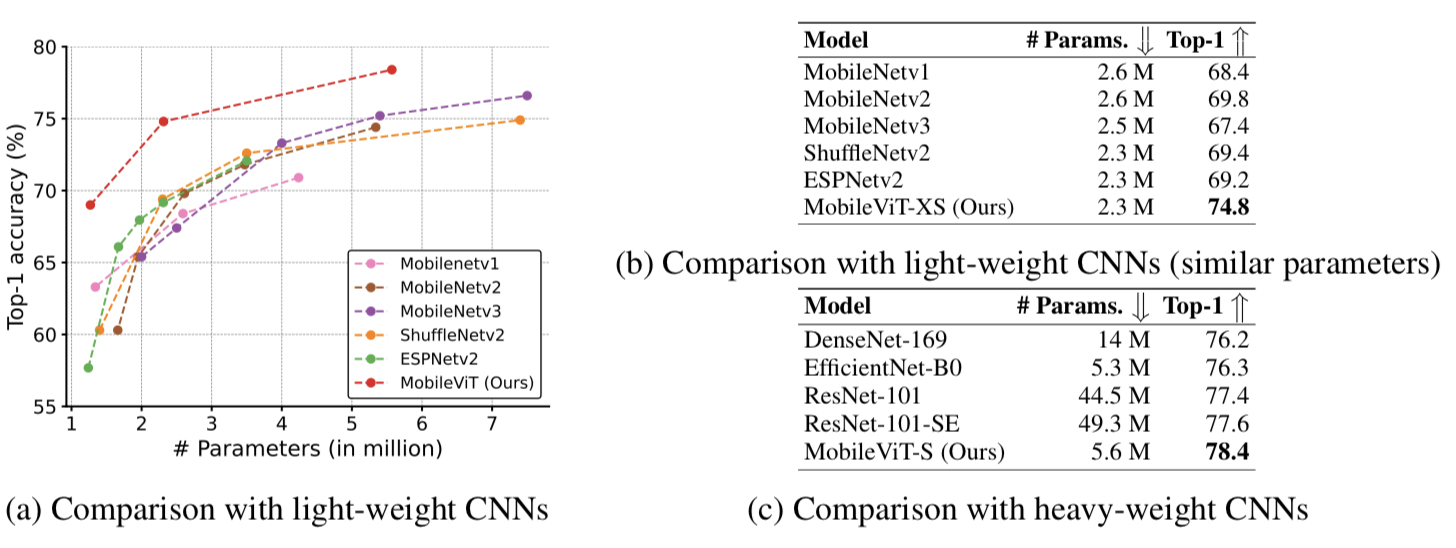
Fig 5에서 볼 수 있듯 MobileViT는 light-weight CNN들 보다 우수한 성능을 보여준다. Fig 5 (b)를보면 MobileViT-XS모델은 파라미터 수는 가장 작지만 top-1 acc 는 가장 높은 성능을 보여 준다. 심지어 Fig 5 (c)를 보면 heavy-weight CNN 네트워크와 MobileViT-S 모델을 비교 해도 상대적으로 작은 파라미터 수로 높은 top-1 acc 성능을 보여 준다.

ViT와 비교:

CNN 계열 네트워크 들과 비교 결과와 거의 유사하다. Fig 6 (a), (b)에서 볼수 있듯이 MobileViT-XS, MobileViT-S 모델은 다른 ViT 모델들 보다 상대적으로 적은 파라미터 수로 더 좋은 top-1 acc 성능을 달성했다.
비교를 위해 ViT 계열 모델들 학습시 advenced augmentation사용, distillation 비사용, MobileVit는 basic augmentation을 사용했다.

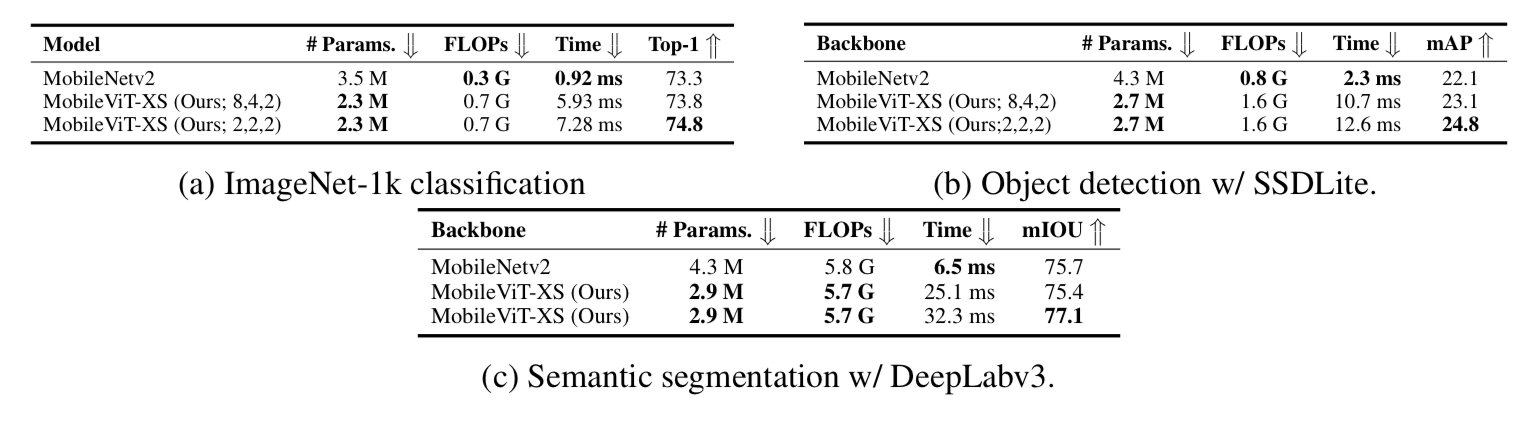
Object detection 과 Segmentation:

아래 그림 Fig 7에서 보듯이 MobileViT는 object detection 과 segmentation task에서도 backbone으로서의 역할을 수행 할수 있고 성능 또한 MobileNetV2에 비해 좋은 결과를 보여준다. 단 inference time이 mobileNetv2가 압도적인 것으로 보이는 데 이것은 MobileNetV2 의 연산은 하드웨어 최적화가 잘되어있기 때문으로 논문의 appendix에 이 부분에 대한 분석이 포함되어있다. 꼭 읽어 보길 바란다. (사실 이유는 이미 언급했듯이 mobilenetv2는 하드웨어 최적화가 잘되어있기 때문으로 MobileViT의 연산을 효율적으로 지원하는 하드웨어 가속기가 존재한다면 MobileViT의 속도도 훨씬 빨라질 것이라고 하는데 이는 모든 구조가 다 마찬가지 아닌가 하는 생각..)

생각 해 볼만 한 사실들

Patch Size:

아래 그림 Fig 8 은 patch size 에 따른 inference 속도 변화 와 acc 성능 변화를 보여준다. patch size 에 따라 inference 속도와 acc 성능 변화가 나타나니 응용에 따라 주의 깊은 튜닝이 필요할 것 같다.

$nxn$ convolution kernel size 와 patch size ($ h \times w$)의 관계:

아래 그림 Fig 9에서 n은 convolution kernel의 크기, h,w는 patch 의 크기를 나타낸다.

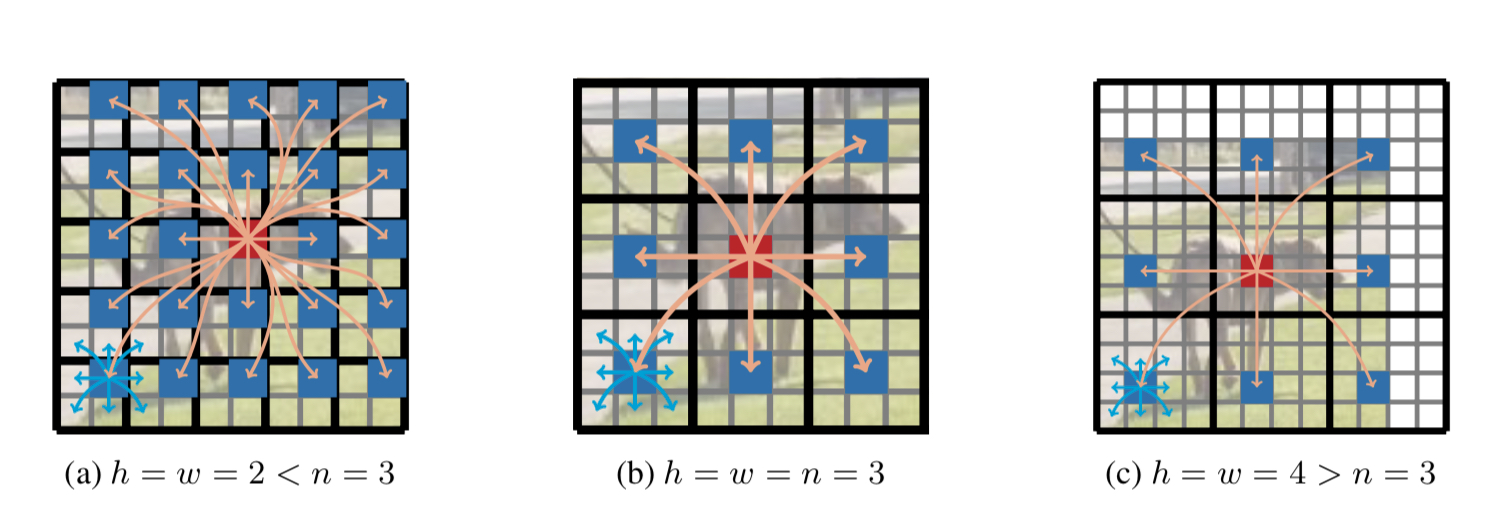
$h or w > n$ 일 경우 Fig 9 (c) patch 내의 각 pixel은 해당 convolution을 통해 patch 에 속한 모든 pixel의 정보를 취합 할 수 없으므로 local information의 취합 능력이 떨어진다. 이는 곳 전체 적인 성능 하락으로 이어진다.

Inference speed:

논문의 제목에서 알 수 있듯이 MobileViT는 edge device 에서 효율과 성능이 좋은 network를 목표로 했다.
하지만 아래 표 에서 보이듯 실제 iPhone 12 cpu, iPhone12 neural engine, NVIDIA V100GPU 에서 inference time을 비교 해보면 MobileNetv2가 위 언급된 모든 device에서 가장 빠르다.

iPhone에선 MobileViT는 DeIT, PiT 보다는 빠르지만 GPU 에서는 DeIT, PiT 가 오히려 빨랐다. GPU에서 MobileViT가 DeIT, PiT 보다 느린 이유는 1) MobileViT 모델이 shallow 하고 narrow 한 특성이 있고, 2) 256x256 이라는 좀더 큰 해상도 (DeIT는 224x224)로 동작 하기 때문이라고 한다. 또한 MobileViT 의 MobileViTblock 에서는 unfolding, folding 연산(Fig 1 참조)이 수행되는데 V100에서 이 두 연산을 gpu -accelerated operation을 사용 하는지 안하는 지에 따라 그 결과가 다르다. gpu -accelerated operation 을 사용 하지 않을 경우 0.62ms 이 걸리고 사용할 경우 0.47ms 이 걸린다. 그리고 MobileNetv2의 inference 속도가 빠른 이유는 mobileNetv2를 구성하는 연산을 서포트 하는 하드웨어 가속기의 덕분일 것으로 본다. MobileViT에 사용 되는 연산들이 하드웨어에 최적화되게 구현된다면 mobieViT의 inference 속도도 더 높아 질수 있을 것이라고 저자는 말한다.


-끝-

참조:
code link: https://github.com/chinhsuanwu/mobilevit-pytorch

오늘 정리할 논문은 swin transformer로 요즘( 혹은 한동안) 핫한 transformer를 비전 테스크에 적용한 논문이다.
기존 CNN 기반의 backbone을 사용하지 않고 순수하게 transformer를 이용해 feature를 이미지에서 feature를 뽑아 낼 수 있다는 것을 보여준다.

Title :

Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

git repo

Contribution

Transformer는 NLP분야에서 LSTM을 대체 할 수 있는 방식으로 연구되다 비전쪽에서도 다양한 문제에 응용되고 있다.
하지만 텍스트와 영상은 그 특성이 서로 다르다. 구체 적으로 영상에 transformer를 적용하는 것에는 다음과 같은 문제를 해결해야 한다고 이 논문에서는 말하고 있고, 각각에 대한 본인들만의 해결책을 재시 했다.

1. word token과 달리 visual element는 scale이 다양하다.
NLP를 정확히 몰라 이부분에 대한 내 이해가 정확한지는 모르겠지만 나름 해석을 해보자면 NLP에서 각 word token은 고정된 크기의 embedding으로 변환 된다. 하지만 이미지는 그 크기가(resolution이) 640x480, 1024X768등 다양할 수 있다. 따라서, 영상에서 NLP의 token과 같은 고정된 크기로 표현 가능한 단위를 설정하는게 필요하다.
-> 일정 한 수의 pixel 집합을 patch라고 정의하고 이 patch를 token처럼 처리의 최소 단위로 정의해 이 문제를 해결

2. 영상은 텍스트에 비해 high resolution이다.
semantic segmentation 같은 경우 pixel 단위의 prediction이 필요 한데 transformer의 computational complexity가 image size에 qudratic 하게 증가 하기 때문에 연산량 증가의 문제가 발생한다.
-> 계층적인 feature map을 이용하고 feature map의 window 내에서 local self-attention을 적용함으로서 complexity 문제를 해결, 각 window에는 일정한 수의 patch 만 포함되도록 설계하여 전체 연산량이 window 수에 선형적으로 증가하게 설계(self-attention 계산 방식의 최적화)

3. self-attention을 ResNet의 spatial convolution 전체 또는 일부를 대체하는 방식이 제안된 적이 있으나 실제 하드웨어에서 latency issue가 발생한다( 이부분은 정확히 이해 하지 못했다. 언급된 방식들의 caching 능력이 떨어진다고 봐야 할 거 같은데... 혹 이 글을 읽고 있는 누군가 이에 대한 답을 안다면 댓글로 설명 좀 해주심이..)
-> shift windows를 사용해 해결

즉 swin transformer 의 key feature는 1. shift window, hierahical patch representation(계층적 패치 표현), 최적화된 self-attention 계산 방식 으로 볼 수 있을거 같다.

구조

이제 swin transformer의 구조를 살펴 보자. 여기서는 아래 그림 Fig1 의 (d)의 전체 구조를 참고해 입력 영상이 각 모듈에 들어가서 연산을 거칠때 어떻게 변해 가는지 그리고 위의 contribution에서 언급한 각 문제점의 해결책이 어느 모듈에서 어떻게, 왜 수행되는지를 정리 할 것이다. 여기서는 숲을 설명하고 나무를 설명하는 방식이 아니라 각 모듈을 나무로 생각하고 나무에 대해서 설명한다. 각 모듈에 대한 설명을 이해하고 Fig1 (d)의 보면 전체적으로 이해 하는데 도움이 될 거라고 생각한다.

Fig1은 swin transformer 의 계측적 구조, shift window, transformer block 내부 구조, 전체 모델의 구조를 보여 준다. 우선 (d)의 전체 구조를 기준으로 살펴 보자.

swin transformer에서는 patch 라는 단위를 NLP의 token 처럼 사용한다. 이 patch를 이용해 고정된 크기의 embedding을 만들어 낸다. patch 라는 용어가 새로 나와 겁먹을 필요는 전혀 없다. 입력 영상에서 4x4 윈도우 내에 들어오는 pixel들을 concat해서 표현한 것이 patch이다.
예를 들어 입력 영상을 HxWx3, patch 크기를 4x4 pixel로 정하면, patch partition은 4x4 크기의 grid셀에서 그룹을 형성하는 pixel들을

와 같이 concat해서 나타낸다. 이렇게 나타낸 patch는 4x4x3=48 의 크기를 지닌다. (4x4는 patch 크기 이고 3은 pixel의 channel 수 이다.) 이렇게 표현된 patch를 embedding으로 표현 하기 위해 linear layer를 이용해 연산한다.

아래 그림 Fig2는 Fig 1. (d)의 patch partition + linear embedding 모듈에서 입력 영상이 어떠한 형태로 변화 되는 지를 간단히 도식화 하고 있다. Fig2 의 가장 좌측 그림을 보면 굵은 선 안쪽에 얇은 선으로 4x4 필셀을 표현했다. 서로 다른 색으로 표혀한 것이 4x4 pixel 그룹이다. 이 4x4 픽셀들을 channel 축으로 concat하고 128channel의 embedding 을 만들기 위해 linear layer에 입력하고 swin transformer block에 입력하기 위해 spatial 축(영상의 가로와 세로) 를 HxW 으로 flatten 해주면 Fig 2의 가장 오른쪽같은 형태가 된다.

다음으로 swin transformer block에서는 multihead attention을 이용한 연산을 수행한다. 블럭 내에서 수행되는 연산은 Fig 1의 (c)를 보면 알 쉽게 알수 있다. (c)에서 W-MSA는 윈도우 내에서 수행되는 multi head self-attention을 의미한고 SW-MSA는 shifted window multi head self-attention을 의미한다.

swin transformer에서 self attention은 non-overlapped window내의 patch만을 이용해 수행된다. 여기서 윈도우란 patch의 집합으로 이해 하면된다. (patch는 인접 pixel의 집합, window는 인접 patch의 집합)

 W-MSA와 SW-MSA가 있는 이유는 input의 크기에 quadratic 하게 증가하는 computational complexity 문제를 해결하기 위해 도입한 window라는 개념 때문이다. 윗 문장에서 말했듯 swin transformer에서 정의하는 윈도우는 non-overlap이다. 즉 윈도우 내에 속한 patch 들 간의 연관성은 self-attention에서 고려 할수 있지만 서로 다른 윈도우에 속한 patch들 간의 연관성을 파악할 수 없다는 문제가 생긴다. 이를 해결 하기 위해 도입된게 SW-MSA(shifted window multi head self-attention)이다. Fig 1.의 (b)가 W-MSA와 SW-MSA에서 feature map을 어떻게 나누는지 보여준다. 우선 Fig 1. (b)의 왼쪽 그림은 사이즈가 4x4인 non-overlapped window로 feature map을 나눴을 때의 경우를 보여 준다(W-MSA에서 연산에 이용하는 window partition 방식이다.) Fig 1. (b)의 오른 쪽 그림은 SW-MSA모듈에서 사용하는 window partition 방식으로 W-MSA에서 서로 다른 window에 속해 있던 patch들이 같은 window로 묶이면서 상호간의 연관성(self-attention)을 고려 할 수 있게 된다.

 SW-MSA를 구현 할때 한 가지 중요한 아이디어가 들어가는데 바로 cyclic shifted window이다. window의 크기와 shifted window의 stride에 따라 영상의 가장자리에 patch들이 window를 가득 채우지 못 할 경우 이를 해결 하기 위해 feature map을 단순히 패딩 하면 연산량이 증가되는 손실을 감수해야 한다. 저자는 이러한 문제를 효율적으로 풀기 위해 feature map을 top-left 방향으로 shift 시켰다. 아래 그림 Fig 3은 이 방식을 도식화해 보여 준다.

Fig 3 의 가장 왼쪽은 partition 된 feature map을 보여주는데 정 중앙에 위치한 M이 속한 윈도우만 실제 윈도우 크기에 부합하고 나머진 partition들은 윈도우의 크기보다 작게 된다. 각 partition을 모두 패딩해서 윈도우 크기인 4x4로 채우는 대신 Fig 3 cyclic shift 에 나타낸 것 처럼 A,B,C를 top-left 방향으로 회전(cyclic shift) 시키면 패딩을 하지 않아도(실제 코드에서는 물론 패딩도 들어간다. 하지만 패딩의 크기는 최소화 된다.) window 크기에 딱 맞는 partition을 만들 수 있다. 단 이렇게 하면 A,B,C는 원래의 feature map 에서 실제로는 서로 이웃 하지 않은 patch들과 같은 window에 속해 self-attention이 계산되는데 cyclic shift 하기 전의 feature map에서 서로 이웃 한 patch들간에만 self-attention이 계산 되도록 mask를 씌워준다. 이렇게 SW-MSA 연산이 끝나면 cyclic shift했던 것을 되돌려 준다. 

W-MSA, SW-MSA에서 또 한가지 언급 할 것은 Relative position bias이다. Attention module 에서는 $\frac{Q \cdot K_{T}}{\sqrtd} +B$ 와 같이 positional bias (B) 를 연산 과정에서 더 해준다. swin transformer에서는 relative position bias를 이용했는데 윈도우 크기를 M 이라 할때 한 윈도우의 각 축으로 방향으로 $ [-M+1, M-1]$의 상대 위치 offset을 정의하고 이 값들로 B를 구성해 positional bias로 이용했다. (transformer에서 positional bias는 매우 중요한 개념이다. 여기선 간단히만 언급 했지만 사용 이유와 의미를 꼭 파악하자. 스스로에게 하는 말이다. ) 

 아래 Fig 4. 은 Fig 1. (d)의 swin transformer block에서 입력이 data가 어떤 모양으로 변하고 어떻게 연산되는지를 간략히 도식화 한 그림이다. patch partition + linear embedding 단계에서 flatten되었던 입력 영상을 non-overlapped window로 분리하기 이해 공간 정보를 복원한다.(공간 정보를 복원한다는건 입력의 shape을 (batch size, HxW, embedding size)에서 (batch size, H,W, embedding size)로 reshape 하는 과정을 말한다.) 그 후 윈도우 크기로 분해된 feature map을 W-MSA또는 SW-MSA의 입력으로 넣어 attention 을 계산 해 준다. 어텐션 과정도 내 나름대로 도식화 했지만 내가 보기에만 좋은 그림 같기도 하다. 혹시 self-attention 연산 과정을 정확히 알지 못하는 독자는 여기 를 참조 하길 추천한다. (나에겐 정말 큰 도움이 되었다.)

그런데 왜 이렇게 window 개념을 도입하면 computational complexity가 줄어드는 걸까?

MSA 연산은 크게 다음과 같은 단계로 구성된다.  -> 다음에 나오는 것은 각 단계에서 이루어지는 연산의 연산량이다.

1. input x와 weight $W_{Q}, W_{K}, W_{V}$를 이용해 $Q,K,V$ 계산

-> $Q = X \cdot W_{Q} => (hw \times C) \times (C \times C) = hw\times C^{2} $

    $K = X \cdot W_{K} => (hw \times C) \times (C \times C) = hw\times C^{2}$

    $V = X \cdot W_{V} => (hw \times C) \times (C \times C) = hw\times C^{2}$ 

2. $Q,K$ 를 이용해 attention score 구하기

-> $A = Q \cdot K^T => (hw\times C) \times (C \times hw) = (hw)^2C$

3. attention score와 $V$를 이용해 값 정재

-> $Z = A \cdot V =>(hw \times hw) \times (hw \times C) = hw\times C$

4. attention 적용된 output $Z$에 output weight $W_{z}$ 적용

-> $ out = Z \cdot W_{z} => (hw \times C) \times (C \times C) = hwC^2 $

이렇게 각 단계의 연산량을 다 더하면 MSA의 연산량은 $\Omega (MSA) = 4hwC^2 + 2(hw)^2C$ 이가 된다. 

그럼 W-MSA 는 어떨까?

위에서 언급한 4단계에서 2, 3단계의 연산량이 아래와 같이 바뀐다. 

2. $Q, K$ 를 이용해 attention score 구하기-> attention score를 윈도우 MxM에서 구하기

-> attention score를 구할때 고려하는 patch수는 hw가 아니라 MxM 즉 $M^2$

    $A = Q \cdot K^T = (M^2 \times C) \times (C \times M^2) = M^{4}C$

3. attention score와 $V$를 이용해 값 정재

-> $ Z = A \cdot V => (M^2 \times M^2) \times (M^2 \times C) = M^{4}C$

다만 윈도우가 $\lfloor \frac{h}{M} \rfloor \times \lfloor \frac{w}{M} \rfloor $ 개 있으므로 

$\frac{hw}{M^2} \times 2(M^4)C = 2M^2hwC$ 가 된다. 

따라서 window multi head self-attention을 적용하면 $\Omega (W-MSA) = 4hwC^2 + 2M^2hwC$ 가 되어 

$M^2 <= hw $ 일경우 연산량이 적어진다. 

마지막으로 계층적(hierachical feature)를 생성하기 위해서 patch merging 모듈에서는 patch의 숫자를 줄인다. 방식은 patch partition 에서 input의 RGB 채널은 concat한 것 처럼

각 stage의 출력을 patch mergin layer에서 2x2 grid 안에 들어오는 즉 서로 인접한 4개의 patch를 채널 축으로 concat 해준다. 

이걸 convolution의 receptive field관점으로 해석 하면 stage 1에서 4x4 가 receptive field이고 stage2dptjsms 8x8, stage 3 에서는 16x16, stage 4에서는 32x32 와 같이 볼 수 있다. Fig 1의 (a)는 이것을 도식화 한 것이다. 

이 논문은 SOLO 논문을 읽다가 알게 되었는데 깊이 생각해 보지 않은 문제에 대해 이슈 제기를 하고 해결법을 

제안해 정리 해 보고자 한다.  

본인이 생각하는 흐름의 자연스러움 때문에 논문의 흐름과는 다른 흐름으로 정리했다. 

paper: 

An intriguing failing of convolution neural networks and the CoordConv solution

문제 제기:

이 논문에서는 coordinate transform 라는 문제를 제기 하고 우리에게 친숙한 convolution이 태생적인 문제(= translation invariant)로

인해 coordinate transform문제에 굉장히 취약 하다는 것을 보였고 CoordConv라는 간단한 개념을 도임해 이를 해결할 수 있다고 주장한다. 

그럼 coordinate transform 이 뭘까 ?

이 논문은 우리가 암묵적으로 convolution을 이용해 굉장히 많이 풀고 있는 문제의 가장 기초적인 두 가지 문제를 convolution이 놀랍도록 못 푼다는 발견에서 시작 한다. 

위에서 말한 두 가지 문제는 coordinate classification, coodinate regressiong 이다. 말이 어려워 보일 수 있는데 위 그림 Figrue 1의 가장 위쪽 그림을 보면 이해가 정말 쉽다. 

coordinate classification 문제는 네트워크의 입력으로 (x,y) 좌표(cartesian coordinate)을 넣고 출력으로 해당 (x,y)좌표에 해당하는 pixel만 1의 값을 갖는( 예를 들어 1이라고 했는데 사실 이 숫자는 background와 구분되기만 하면 된다. class 라고 보면 된다.) 이미지를 출력하는 문제이다. 

즉 좌표가 주어졌을때 해당 좌표에 흰색 점을 하나 찍은 이미지를 그려주는 문제가 coordinate classification이다. 

다음으로 coordinate regression 문제는 coordinate classification 문제와 입력과 출력이 바뀐 문제이다. 

즉 입력으로 특정한 한 픽셀만 1의 값을 갖는 이미지를 입력으로 넣었을 때 해당 픽셀의 (x,y)좌표(cartesian coordiante)를 출력으로 내놓는 문제이다. (object detection 이 익순한 분들은 이 문제가 object detection의 bbox regreesion 문제나 key point estimation 문제와 같다는 걸 바로 알수 있을 거다.)

이 두 문제의 정의를 이해 했으면 아래 내용은 정말 간단히 쉽게 이해 할 수 있다.

(참고로 본래 논문에서는 GAN 의 mode collapse 문제도 다루고 figure 1의 가장 아래 그림도 이에 대한 내용인데 이 문제에 대한 설명은 이 포스팅에서는 최소화 하겠다.)

Convolution은 뭘 못하는가?

Convolution이 뭘 못하는지 보기 전에 convolution의 무능을 입증하기 위해 어떤 데이터 셋을 사용 했는지 보자.

Figure 2의 (a)에는 총 9 개의 샘플 이미지가 있다. 각 이미지는  64 x 64 크기이고 단 1 픽셀을 제외한 모든 픽셀의 값이 0이다. 즉 64 x 64 사이즈의 이미지에서 오직 1픽셀만 target인 one-hot encoding 된 이미지라고 볼 수 있다. 

(구태여 부연 설명을 하자면 왜 one-hot encoding이냐면 64x64 = 4096으로 vector로 표시 할수 있다. 

4096 length의 vector에서 오직 한 element만 값이 1 이라고 생각해 보면 이게 one-hot encoding 이라는 걸 알수 있다. )

(a)를 이해 했으면 (b)를 보자.  Figure 2. (b)의 윗줄에 있는 두 그림은 (a)처럼 one-hot encoding된 이미지를 train set, test set으로 나누고 각 데이터 셋에 해당하는 이미지를 모두 합해 하나의 이미지에 나타낸 것이다. 말이 이해가 잘 안될 수 있으니 아래 그림 Figure 3을 보자.

 Figure 3에서 화살표 왼쪽에 있는 그림을 3x3사이즈의 one-hot encoding 이미지라 하자.

이 이미지들을 다 더하고 나면 화살표 오른쪽의 결합 이미지가 된다. 

Figure 3의 화살표 왼쪽에 있는 이미지가 Figure 2의 (a)에 표시된 sample이미지에 대응 되고 화살표 오른 쪽에 있는 이미지가 Figure 2 (b)에 있는 합 이미지 이다. 

다시 Figure 2의 데이터 셋을 설명하면 논문의 저자는 train-test data set 을 두 가지 기준으로 분리했다. 

train-test data set pair 1, train-test data set pair 2를 만들고 각각의 train set을 이용해 학습 하고 test set으로 테스트 했을 때 어떤 결과가 나오는지 보였다. 

1. train-test data set pair 1: 1값을 가지는 pixel이 이미지의 아무 곳에나 위치 할 수 있게 하고 train과 test 셋을 uniform distribution 을 이용해 구분했다. Figure 2 (b)의 윗쪽 두 이미지가 각각  train, test data set을 하나의 이미지로 합친 그림이다. 

2. train-test data set pair 2:  image를 4개의 사분면으로 나누고 1,2,3 사분면에 값이 1인 pixel이 위치한 one-hot encoding 이미지는 train set으로 사용 하고 4 사분면에 pixel 값이 1인 point가 위치한 경우는 test 셋으로 사용 하는 경우이다. (이 경우 네트워크는 학습시 4사 분면에 위치한 sample을 본적이 없기 떄문에 4분면에 위치한 point에 대해 coordinate classification문제를 풀수 있을까?)

데이터 셋 설명이 장황해 졌는데 위 두 데이터 셋으로 coordinate classification 네트워크(일반 convolution 사용)를 학습해 보면 아래 Figure 4와 같은 결과가 나온다. 

Figure 4의 (a) 그래프는 train-test accuracy 의 경향을 보여준다. 그래프의 좌상단을 보면 uniform ○, quadrant ■이라는 걸 보수 있는데 

uniform ○ 은 위에 설명한 train-test data set pair 1로 학습-테스트를 진행한 결과 이고

quadrant ■ 는 train-test data set pair 2로 학습-테스트를 진행한 결과 이다. 

(헷갈리면 반드시 위에 가서 train-test data set pair에 대한 설명을 다시 확인하고 올것.)

uniform 한 데이터 셋을 사용한 경우 학습과 테스트시 그나마 어느정도는 비슷한 accuracy 경향성을 보이지만 (사실 경향성이라고 말하기 힘들다) quadrant 한 데이터 셋을 사용 한 경우 train에 오버 피팅되는 것을 볼수 있다. 즉 quadrant 데이터 셋의 경우 학습 시 네트워크는 1,2,3 사 분면에 target이 위치한 경우만 볼수 있고 테스트시에 처음 4사분면에 잇는 target을 보면 정신을 못 차린다는 것이다. 

다음으로 Figure 4 (b)는 uniform 하게 train-test data set을 나누고 학습 했을때 학습시간에 따라 test accuracy를 도식화 한 그래프 인데 그 값이 86%를 넘어가지 않는다.

즉 여기서 우리가 알 수 있는건 (저자가 말하고자하는 바는) 기존의 convolution은 이 단순한 문제(coordinate classification, coordinate regression)를 정말 심각할 정도로 못푼다는 것이다. 

CoordConv:

바로 위에서 convolution이 뭘 못하는 지를 봤다. 이번엔 그 문제를 저자가 어떤 아이디어로 해결하는지를 보자. 정말 단순하고 간단하다. 

Figure 5의 왼쪽엔 기존의 convolution이 나와있다. 그리고 오른쪽엔 논문에서 제안하는 CoordConv이다. 

CoordConv의 아이디어는 Convolution이 translation invariant한 특성이 있으니 위치에 대한 정보를 알려줘서 신경 쓰게 하는 것이다. (solo 논문에서는 이걸 "coordinate aware" 라고 표현했다.)

이를 위해서 coordconv의 입력 tensor 크기에 대응 하는 좌표를 (-1,1)로 normalize해서 concat 하는 것이다. 이것도 말로 하면 어려운데 코드를 보면 직관적이다. 

x_range = torch.linspace(-1,1, inputTensor[1].shape[-1]) # inputTensor의 0번재 dimension은 batch
y_range = torch.linspace(-1,1, inputTensor[1].shape[-2]) # inputTensor의 0번재 dimension은 batch
y,x = torch.meshgrid(y_range, x_range)
y = y.expand([batchSize, 1,-1,-1]) # j coordinate in Figure 5
x = x.expand([batchSize, 1,-1,-1]) # i coordinate in Figure 5
normalized_coord = torch.cat([x,y],1)
new_feature = torch.cat([features_normalized_coord],1)

위 코드에서  y,x는 각각 Figure 5 오른 쪽의  i cooridnate, j coordinate에 대응 하는 것이고

new_feature는 Figure 5 의 CoordConv에서 concatenate Channels 바로 다음의 $ h \times w \times c+2 $ shape을 가지는 tensor에 해당한다. 

결과:

Figure 6는 Figure 4와 같은 이미지이다. 위의 "Convolution은 뭘 못하는가?"란에서 설명한 두 데이터 셋 

uniform(train-test data set pair 1), quadrant(train-test data set pair 2) 에 대해 CoordConv가 어떤 성능을 보이는 지 보자.

Figure 6의 왼쪽 아래 그림에서 보면 train accuracy와 test accuracy가 일치 하는것을 볼 수 있고 오른쪽 그래프를 보면 학습 시간이 25초만 되도 convolution과 달리 accuracy가 1까지 올라간다.

Figure 번호가 햇갈릴수 있음에도 불구하고 위 figure 7 은 원 논문의 caption을 같이 올렸다. (설명이 햇갈리시면 영문을 읽는게 더 쉬울수 있으므로..)

Figure 7의 왼쪽은 coordinate classification의 학습데이터(가장 왼쪽 줄)와 테스트 inference결과(붉은 색 박스 안쪽)를 보여준다. coordinate classification는 앞에서 설명 한것 처럼 (x,y)를 입력 했을때 이미지에 해당하는 pixel에 색을 칠하는 문제이다. 붉은 박스의 가운데 그림이 convolution으로 inference한 결과를 시각화 한건데 제일 윗줄에 있는 GT 이미지에 4사분면이 가득 차 있는 것과 달리 4사분면이 거의 비어있는 것을 볼 수 있다. 

반면 CoordConv는 4사분면에 있는 점들을 잘 그리고 있다. 

Figure 7의 오른쪽은 coordinate regression을 학습한 결과를 시각화 한것이다. (coordinate regression은 one-hot image를 입력으로 넣고 target pixel의 (x,y)를 출력하는 문제이다. 시각화 한건 출력인 (x,y)를 다시 이미지에 표시한 것이다.)

파란색 박스 안쪽을 보면 convolution은 train데이터에 대해서도 test데이터에 대해서도 추정한 결과가 울퉁불퉁 한 반면, CoordConv는 결과가 GT와 거의 일치 한다. 

정리:

Convolution이 어떤 취약점을 가지고 있는지 비교적 간단한 실험을 통해 알아 보고 이 문제를 해결하기 위한 방법 정리해봤다. 

내 입장에서 CoordConv가 효과를 발휘 할 수 있는 문제는 어떤 식으로든 image로 부터 좌표를 추측하는 문제 즉 object detection일거 같다. 논문의 결과에도 object detection에서 (mnist data셋 기준) 상당한 성능 향상을 보았다고 리포팅했다. 

CoordConv를 사용해도 효과가 없는 문제는 object의 위치와 관련 없는 문제 즉 classification문제 이다. 

위에서 언급은 안했지만 논문을 보면 저자는 mode collapse에 대한 이야기도 하지만 이 포스트에는 정리하지 않았다. 당장의 내 관심사와는 좀 거리가 있고 내 이해가 부족하기도 해서이다. 

오늘 정리할 논문은 one stage instance segmentation 네트워크 인 SOLO이다. 

Paper:

SOLO: Segmenting Objects by Locations

이 논문은 e2e로 학습도 가능 하고 instance를 구분 하는 방식이 매우 흥미 롭다.

SOLO의 접근 방식:

SOLO에서 해결하고자 하는 건 instance segmentation 이다. 

이미지 상에 존재하는 여러 물체를 각각 구분해 mask를 생성하는 문제이다. 

이를 위해 SOLO에서는 object center와 size정보를 이용한다. 

bbox 예측이나 post processing을 통한 instance pixel grouping없이 개별 object를 위 언급한 object center와 size를 이용해 정의한 center region와 해당 region에 대응 하는 mask로 직접 instance mask를 생성한다. 

간단히 기존 instance segmentation 네트워크의 전략을 살펴 보면 크게 top-down, bottom-up 방식으로 나눌 수 있다.

• top-down 방식:  bbox 찾고 해당 bbox 안에 있는 object mask를 생성. 이 방식에서 instance의 구분은 bbox거의 전적으로 의존하게 된다. 
  대표적인 모델은 Mask-RCNN, PANet(mask-rcnn에서 feature representation을 강화한 방식, Mask-scroing rcnn(mask prediction의 품질을 평가하기 위한 mask-iou branch를 도입)
• bottom up 방식: 이 방식의 네트워크 들은 대부분 각각의 object를 구분하기 위해 bbox를 사용하는 대신
  각 object를 구분할 수 있는 임의의 latent space에서 각 object를 나타내는 pixel embedding(의 형태는 다양 할 수 있다.)을 학습하고 post processing을 통해 grouping 한다. 
  대표적인 모델은 
  1. SGN: instance segmentation을 단계적인 sub-grouping문제로 정의. break point 라는 개념을 도입해 각 instance의 경계에 있는 point를 찾고 이 point를 line segment로 line segment를 instance를 grouping해 instance를 구성한다. 
  2. SSAP(single shot instance segmentation with affinity pyramid): pixel이 같은 인스턴스에 속하는 지를 pixel pair affinity라는 확률 값을 계산 하는 문제로 정의

SOLO는 bbox를 찾지도 pixel embedding을 학습해 후처리로 그룹핑 하지도 않고 mask 를 바로 생성하기 떄문에 

Direct mask prediction 이라고 할 수 있다. 

SOLO Architecture:

Fig 1. 은 매우 직관적으로 solo의 framework을 이해 할 수 있다. 

전체 흐름을 간단히 보면 입력 이미지를 SxS grid로 나타내고 어떤 object의 center가 특정 grid cell에 위치하면

그 cell이 sementic category와 instance mask를 예측하는 책임을 진다. 

Sementic Category:

sementic category는 object의 class를 예측하는 branch이다.

Object class 가 c개 있다면 category branch는 $ S \times S \times C$ 형태의 tensor를 생성한다.  이때 grid cell (i,j)에 있는 길이 c의 vector는 해당 cell에 object center가 존재하는 객채가 어떤 class에 속할지 에 대한 확률값 벡터이다. 

Instance mask:

Instance mask head의 output shape은 $ H \times W \times S^2 $  이다.

채널이 $ S^2 $ 인 이유는 grid cell (i,j) 각각에 대응 하는 채널이 하나씩 있기 때문이다. 

즉 Intance mask의 각 채널은 category branch의 grid cell (i,j)와 1:1 매핑 되는 관계이다.

예를 들어 임의의 객체 A의 center가 grid cell (i,j)에 위치 한다면 이 객체의 segmentation mask는 

$ mask channel = i \times S + j$ intance mask 에 생성되게 끔 네트워크를 학습한다. 

Fig 1.의 input image와 category branch 를 보면 왼쪽 얼룩말의 센터는 grid cell에서 붉은 색$(i_{1}, j_{1})$으로, 오른쪽 얼룩 말의 센터는 grid cell에서 파란색$(i_{2}, j_{2})$으로 표시 된다. 그리고 이 두 얼룩말의 마스크는 각 grid cell에 대응 하는 intance mask channel $ i_{1} \times S + j_{1}$, $ i_{2} \times S + j_{2}$에 각각 생성되는 식이다. 

이렇게 grid cell 위치와 instance mask 채널이 서로 연관되어 있기 때문에 SOLO는 "coordinate aware" convolution을 사용 했다고 한다.(기존 convolution은 translation invarian한 특성을 가지고 있기 떄문에 이와는 구분된다.)

그리고 이를 위해 CoordConv라는 convolution을 사용 했다. 

CoordConv는 instance mask branch의 입력과 같은 spatial size를 갖는 $ H \times W \tmes 2$ 크기의 텐서에 coordinate을  [-1,1]로 normalize하고 backbone의 output에  concat해서 instance mask branch에서 사용 한다. 

Fig 2의 Mask branch에서 input channel이 (256+2)인 이유가 바로 이 coordinate 정보를 concat했기 때문 이다. 

아래 코드를 보면 쉽게 이해가 된다. 

$코드 입력$

FPN:

SOLO는 feature pyramid layer(FPN)의 output이 각 category branch와 mask branch의 입력으로 사용되어 서로 다른 크기의 object를 찾는 효율을 높였다. 

학습:

GT 생성: 

 intance mask를 category classification grid cell위치에 대응 하는 instance mask channel에 binary mask 형태로 생성한다. 따라서 학습시 instance mask를 이에 대응 하는 형태로 만들어야 한다.

 앞서 object center가 (i, j) grid cell에 위치한다고 할때 해당 cell 이 object의 class와 mask생성을 담당한다고 했다. 이때, object size에 따라 여러 cell이 한 object의 class와 mask생성을 담당할 수도 있다. object center 좌표는 object mask gt 의 centre of mass로 정의하고 object 크기를 고려해 center sampling을 하기 위해 center region은 $ (C_{x}, C_{y}, \epsilon W, \epsilon H) \epsilon=0.2$ 로 정의한다. 

 이렇게 center region을 정하고 나면 category grid cell 상에 아래와 같이 center region이 형성될 수 있는데 이때 각 cell 위치에 해당하는 instance mask channel의 binary mask가 똑같이 들어간다. 

Fig 3은 이해를 돕기 위해 그린 그림이다. 붉은 색영역은 임의의 object에 대한 center region 이고 이에 대응 하는 mask gt가 intance mask gt에 어떻게 저장되는지 보여 준다. 

LOSS:

$$ total loss = L_{category} + \lambdaL_{masks} $$

Category classification($L_{category}): 

solo는 category classification을 위해 focal loss를 사용 했다. (굳이 식을 설명하지 않아도 될정도로 많이 사용되니 식은 생략한다.)

Segmentation Mask($L_{masks}$):

Dice loss:

$ L_{mask}= \frac{1}{N_{pos}} \sum I(p_{i,j} >0) d_{mask}(m_{k},m_{k}^{*}) $

$ d_{mask}=1-\frac{2\sum_{x,y}(p_{x,y},q_{x,y}}{\sum_{x,y}p_{x,y}^{2}+\sum_{x,y}q_{x,y}^{2}} $

$p_{i.j}$ 는 category target으로 i,j는 grid cell 상의 좌표.

$m_{k}^{*}$는 mask gt

$d_{mask}$에서 $p_{x,y}$는 mask prediction 에서 x,y위치의 pixel value, $q_{x,y}$는 gt mask의 pixel value이다. 

Inference:

inference 시 category score threshold는 0.1을 사용해 낮은 score를 필터링 하고 score상위 500개에 대응되는 mask에 NMS를 적용한다. 

최종 score를 계산하기 위해선 maskness를 category score에 곱해 주는데 maskness란 $\frac{1}{N_{f}\sum p_{i}}$로 표현되고 $p_{i}$는 prediction mask의 pixel value 다. 

(mask ness 를 곱해주는 의미는 maskness점수가 높다는게 곧 해당 object의 형태를 잘 찾았다는 것일 태니 그걸 최종 score에 반영하는 것 같다. )

결과:

Fig 4.에서 볼 수 있듯이 SOLO는 Mask R-CNN과 비슷 하거나 더 좋은 결과를 보여 준다. one stage instance segmenation이 two stage보다 좋아 질 수 있다는 충분한 가능성을 보여주는 예시 인거 같다. 

가장 좋은 성능을 보인것은 Resnet 101 backbone+ deformable convolution+ FPN을 사용 한 모델이다. 

Fig 5에서는 SOLO가 어떻게 동작 하는지를 볼 수 있는데 아랫 줄의 보라색은 category branch 의 grid 가 12 x12일때

대응 되는 instance mask branch의 각 채널이 어떤 prediction결과를 가지는 지 보여준다. 

 instance mask branch output의 각 채널은 하나의 object에 대응 하는 mask를 생성하는 것을 볼 수 있는데 이 mask는 해당 채널과 대응 하는 category branch의 grid cell에 center가 위치하는 객채의 마스크 이다. 

객체의 크기에 따라 center region 이 여러 cell을 포함 할 수 있기때문에 대응 되는 intance mask channel도 여러개 일수 있어서 한  object의 mask가 여러개 생성되는 모습을 볼 수 있는데 NMS를 이용해 같은 객체의 mask를 하나로 합친다. 

Fig 6은 category branch의 grid size에 따른 AP 결과를 보여 준다. grid number 12,24,36은 단일 grid size를 사용 했을 경우를 말하고 Pyramid는 FPN을 사용해 여러 grid size를 사용해 결과를 추정 했을때를 말한다. 

단일 size이 grid를 사용할 경우 grid size가 클수록 AP가 높게 나왔고 FPN을 사용해 여러 grid size를 고려 하는게 가장 높은 결과를 모여준다. FPN의 경우 다양한 object 크기를 고려 할 수 있으니 당연한 결과로 생각된다. 

Fig 7은 coordinate aware convolution 이 결과에 어떤 영향을 미치는지에 대한 테스트 이다. 

Coordconv 를 사용 하지 않을 경우 Fig 7 테이블의 가장 윗줄의 AP =32.2가 coorconv를 사용했을 때보다 최소 3.6point가 낮은 결과를 보여 준다. 비슷 하게 coordconv를 2회 이상 사용하는 것은 성능에 영향을 거의 미치지 않는 것을 볼 수 있기 때문에 논문에서는 2회만 사용 했다. 

논문에서는 좀더 많은 ablation experiment를 진행했지만 이정도만 정리해도 충분할거 같다. 

coordConv의 내용이 좀 흥미로워서 이 논문을 한번 읽어봐야겠다.

오늘은 리뷰할 논문은 FCOS: fully convolution one-stage detection 이다. 

제목에서 알 수 있듯이 one-stage detector 이다. 

Title: FCOS: Fully Convolution One-Stage Detection

link: https://arxiv.org/abs/1904.01355

요약:

자세히 살펴 보기전에 FCOS의 컨셉을 간단히 요약 하자면 저자는 anchor-based one stage는 training 할때 anchor box overlab의 해결하는데 시간이 오래 걸리므로 anchor-box free한 detector를 제안한다. Anchor box를 제거한 detector에서는 low recall rate, ambiguous sample 문제가 발생할 수 있는데 이런 문제를 해결할 수 있는 구조를 제안하고 해당 구조에 대한 효율성을 실험을 통해 입증했다. (문제를 해결하는데 사용한 개념은 FPN(feature pyramid network, per-pixel estimation, center-ness 등으로 아래에서 자세히 살펴 본다.)

Contribution:

1. Detection 문제를 segmentation 문제 처럼 per-pixel prediction 문제로 정의 하고이에 대한 구조를 제안함

2.  FCN(fully convolution network)을 사용해 문제를 해결함으로서 다양한 테크닉을 segmentation에서 사양하는 다양한 테크닉을 공유 해서 사용할 수 있다(고 주장함)

3. proposal free, anchor free 하게 문제를 정의 함으로써 hyper paramter의 개수를 줄임(사람에 대한 의존성을 줄인것이므로 이건 확실한 기여점이라고 개인적으로 생각한다.)

4. anchor box와 관련된 연산 감소(anchor box-GT box간의 매칭등에 소요 되는 연산량 감소)

5. One-stage로서 SOTA(state-of-the-art) performance를 이뤘고 2 stage detector에서 RPN으로 사용해도 anchor-based RPN보다 성능이 좋다. 

6. 확장 가능한 모델이다.(이 논문에서는 Detection 문제가 타겠이었지만 instance segmentation, key-point detection 등으로 쉽게 확장 가능 하다(고 주장한다.). FCN base 이므로 이 말을 맞는 말일거 같다.)

Anchor-based detector의 문제 점들

Anchor-based detector가 가지는 문제는 크게 hyper parameter에 관련된 문제, negative-positive sample의 imbalance에 대한 문제, computation(연산량) 문제로 나눠 생각 할수 있다. 

1. hyper parameter 관련 문제

• anchor의 수, 사이즈, aspect ratio등은 predefined되어 있는데 이에 따라 성능에 영향을 쉽게 받는다.(수작업으로 튜닝 해야 하는 파라미터의 개수가 많다)
• box scale과 aspect ratio가 고정이라서 다양한 모양을 가지는 small object에는 태생적으로 비효율 적이다. 

2. sample imbalance 문제

• High recall rate을 달성하기 위해선 anchor box를 dense하게 배치 해야 하는데 이경우 많은 anchor box가 negative sample로 label되고 이는 학습 중 negative-positive sample 불균형을 악화 시킨다. 

3. 연산량 문제

• anchor box는 IOU계산을 위해 predicted box-GT box간에 매칭을 해야 하는데 이때 발생하는 연산량이 비효율 적으로 많다.

기존 Anchor free detector들이 가지고 있던 문제 점들 

1. YOLO1은 낮은 recall rate을 보여 주는데 이건 object center 근처에 있는 몇몇 points들만 bbox 예측에 이용했기 때문이다. (object를 감싸는 bbox내에는 굉장히 많은 point가 있는데 그중 center 근처의 몇몇 개만 이용하는게 문제라고 주장함)

2. CornerNet에서는 같은 instance에 속한 left-top, right-bottom corner pair를 찾기 위한 추가 metric을 학습하고 post processing을 이용해 이들을 grouping 하므로 연산량이 많아져 비효율 적이다.

3. Dense Box 기반의 모델들은 overlapping bbox, 낮은 recall rate등의 문제로 인해 일반적인 object detection task에 부적합 하다고 여겨졌다.

FCOS의 전략

본 논문에서는 위에서 언급된 anchor free detector들이 가지고 있는 문제들을 per-pixel prediction과 FPN을 이용해 해결하고, 제안하는 구조에서 발생한 low quality bbox prediction문제를 해결하기 위해 center-ness score layer를 도입했다. 

1. Per-Pixel prediction

 - Anchor-based detector 들은 feature map의 각 픽셀 위치를 object center라고 가정하고 미리 정한 size의 box를 regression 한다. 이중 IoU가 낮은 bbox들은 negative sample이므로 실질적으로 학습과정에서 object의 위치를 추정하는데 사용되는 픽셀은 object center 근처에 있는 픽셀들이 전부라고 할 수 있다. 

저자는 이게 문제라고 생각하고 FCOS에서는 feature map의 모든 픽셀 위치에서 해당 픽셀이 특정 object에 속한 픽셀인지 아닌지, object에 속한 픽셀이라면 해당 픽셀에서 예상한 bbox는 무엇인지를 계산하는 방식이다. 

예를 들어 아래 그림이 feature map이라고 한면 이 논문이 제안하는 방식은 p1,p2,p3 및 노란박스 영역에 속한 모든 pixel들은 노란박스가 나타내는 object에 해당 하는 픽셀이므로 해당 픽셀들 각각에 대해 (마치 sementic segmentation과 같이)픽셀이 속한 class label을 예측하고, 각 위치에서 object bbox를 regression한다. 

이런 방식으로 feature map의 모든 픽셀에 대해(Fig1에서는 $p_{1},p_{2},...,p_{n}$ 전부에 대해) 해당 픽셀이 속한 class $c^{(i)}$, bbox 추측을 위한 4개의 값 $(l^{*},t^{*}, r^{*}, b^{*})$을 추정하도록 네트워크를 구성했다. 그러니까 한 픽셀당 $ (l,t,r,b,c)$ 5개의 값을 예측 하는 것이다. 

이때 feature map 상의 픽셀 $(x,y)$가 라벨이 $c^{*}$인 object bbox 내부에 있는 픽셀이면  target label은 $c^{*}$로 정의 하고 positive sample이라고 보며 object bbox내부에 있는 픽셀이 아니라면 target label $c^{*} =0$ 이 되어 negative sample 로 정의 한다. 

bbox 예측에 사용되는 target $(l^{*},t^{*}, r^{*}, b^{*})$ 각각은 feature map상의 위치 $(x,y)$에 대해 해당 픽셀이 포함된 object bbox의 $(좌측 면, 위쪽 면, 오른쪽 면, 아래쪽 면)$  까지의 거리(단위pixel)에 해당하는 값으로 각각은 GT bbox 정보로 부터 아래와 같이 계산된다. 

$$ l^{*}=x-x_{0}^{(i)}, t^{*}=y-y_{0}^{(i)}, r^{*}=x_{1}^{(i)}-x, b^{*}=y_{1}^{(i)}-y             Eq(1)$$

위 식에서 $(x,y)$는 feature map 상의 위치, $(x_{0}^{(i)},y_{0}^{(i)})$는 object bbox의 left-top corner 좌표,  $(x_{1}^{(i)},y_{1}^{(i)})$는 object bbox의 right-bottom corner 좌표를 의미 한다.

$(l,t, r, b)$를 network에서 예측 한 후 IoU를 계한 하기 위한 $(x_{0}^{(i)},y_{0}^{(i)},x_{1}^{(i)},y_{1}^{(i)})$복원은 $Eq(1)$이용해 쉽게 가능하다. 

각 기호에 대한 정확한 의미는 아래 그림(Fig2.)를 참조 하면 더 직관적이다. 

특이하다고 생각 한 점은 각 픽셀의 class label $c$를 추측 하기 위해 multi class classification 컨셉을 사용 하지 않고 각 object class별로 binary classification으로 학습했다는 것이다. 

무슨 말이냐면 예를 들어 MS coco data 의 경우 object 카테고리가 80개 있다고 하면 class inference를 위한 network output은 총 80개의 channel로 구성될 것이다. 이때 channel 0은 vehicle, channel 1은 pedestrian, channel 2는 의자 등등이라면  임의의 $(x,y)$ 픽셀이 class 0 일 확률, class 1일 확률, class 2 일 확률을 채널축을 softmax를 취해 구하는 방식이 아니고, 각 channel을 별개로 보고 channel 0 에서는 vehicle에 속한 pixel과 그렇지 않은 pixel, channel 1 에서는 pedestrian에 속한 픽셀과 그렇지 않은 픽셀등을 각 채널 마다 binary classification loss를 구했다는 얘기이다. 

참조: bbox regression을 할떄 네트워크에서 추측한 $(l,t, r, b)$는 target 인 $(l^{*},t^{*}, r^{*}, b^{*})$ 을 regression 하는데 바로 사용되지 않고  실제로 $exp^{(s_{i}l)}$로 사용 되는데 이는 network에서 나오는 $(l,t,r,b)$이 큰 값을 갖게 하고 싶지 않아서 사용 하는 테크닉으로 $(l,t,r,b)$가 상대적으로 작은 값이어도 $exp^{(s_{i}l)}$은 큰 값이 되서 비교적 scale이 큰 $l^{*}$을 추정 할수 있기 때문이라고 한다. 

Loss function:

$L_{cls}$는 $focal loss$, $L_{reg})는 $IoU$ loss를 사용 했다.  $N_{pos}$는 positive sample 수이다.

본 논문에서 $\lambda=1$로 세팅했다.  

2. Multi-level Prediction with FPN 

이 논문에서 제안하는 FPN의 구조는 아래와 같다. 

FPN(feature pyramid network)은 아래와 같은 FCOS의 weak point를 개선한다. 

weak point 1: final feature map 이 큰 output stride를 가질때, 작은 물체들은 해당 feature map에서 표현이 안될 수 있어서 찾는게 불가능 하므로 recall을 낮게 만드는 원인이 된다. 

weak point2: GT bbox 가 겹칠 경우 (Fig2. 오른쪽 overlapped region 참조) "overlap된 구간에있는 pixel들은 어떤 겹쳐진 두 bbox에 둘다 속하는데 어느 object의 bbox와 class를 타겟으로 학습해야 하는가?" 에 대한 문제가 생김

FPN을 이용 하면 서로 다른 size의 feature map을 만들 수 있는데 각 feature map에서 서로 다른 크기의 물체를 찾으면 위 약점들을 해결할 수 있다. 

weak point 1 해결되는 이유: FPN에서 생성되는 feature map은 서로 다른 output stride를 가지므로 작은 output stride를 가지는 feature map에서 작은 물체를 찾고, 큰 output stride를 가지는 feature map에서

큰 물체를 찾으면 해결가능

weak point 2 해결되는 이유: 저자의 관찰에 따르면 overlap은 대부분 bbox의 크기 차이가 상당한 object들간에 발생하는 경우가 대부분이라고 한다. 따라서 overlap을 생성하는 겹쳐진 물체는 서로 다른 feature map에서 찾게 끔 되므로 overlap 문제를 상당부분 해결 할 수 있다. (예를 들면 Fig2. 오른 쪽에서 사람은 feature map P3에서 찾게 끔 할당되고 테니스 라켓을 P5에서 찾게 끔 할당되게 된다는 의미이다.)

 정리하자면 Fig. 4 의 feature map $P_{3},P_{4},P_{5},P_{6},P_{7}$ 각각에서 찾아야 하는 object의 크기를 제안해 놓고 각 feature map에서 찾아야 하는 크기에 해당하는 object만 해당 feature map에서 detection된 object의 positive sample로 사용 하는 것이다. 

이걸 정리하자면 $i ={ 3,4,5,6,7}$ 이 feature map $P_{i}$의 레벨을 표현할때 각  $P_{i}$에서는 아래 조건에 해당하는 크기의 object를 positive sample로 학습하도록 한 것이다.  

$$m_{i-1} \leq max(l^{*},t^{*},r^{*},b^{*}) \leq m_{i}$$

논문에서 실제로 사용한 $m$ 값은 $\{m_{2},m_{3},m_{4},m_{5},m_{6},m_{7}\} =\{0,64,128,256,512, \infty\}$ 이다. 

3. Center-ness

FPN을 이용하고도 FCOS는 anchor based detector들 보다 성능이 떨어졌는데 이 원인은 object center에서 멀리 떨어진 location에서 bbox prediction이 좋지 않아서 였다. 예를 들자면 아래 Fig.5 에서 붉은 점 위치의 pixel에서 검은색에 해당 하는 bbox를 regression 할때 그 예측값 $(l,t,r,b)$가 썩 좋지 않다는 것이다. 

이런 문제를 해결하기 위해 object의 bbox를 결정할때 object center에서 멀리 떨어진 위치에서 예측된 값들의 영향성을 줄이기 위해 아래와 같이 center-ness 를 예측하는 layer를 추가해 이문제를 해결했다. 

center-ness는 Fig4에서 보면 알수 있듯이 classification output과 같은 head에서 계산된다. 

$$ center-ness^{*} = \sqrt{\frac{min(l^{*},r^{*})}{max(l^{*},r^{*})} \times \frac{min(t^{*},b^{*})}{max(t^{*},b^{*})}} $$

이렇게 계산된 center-ness의 heatmap은 아래와 같다. 

실험:

Setting:

backbone: resnet-50

weight initialization: pretrained with imagenet (newly added layer: same as RetinaNet)

batch:16

optimizer: SGD

initial learning rate: 0.01, 0.001, 0.0001( 0.001, 0.0001은 각각 60k, 80k iteration에서 적용함)

input image size: $max(h,w) \leq 1333$, $min(h,w) \leq 800$

BPR성능:

Anchor based detector에 비해 BPR(best possible recall)이 낮을 것이라는 예상과 다르게 FCOS는 Fig7.의  table 1에 보이듯 $P_{4}$feature map 만 사용 한경우에서 조차 95.55%의 recall rate을 보여준다. 

FPN을 사용 하면 98.4%로 $IoU \geq 0.4$ 인 경우만 고려했을 경우 Anchor base detector인 RetinaNet(with FPN)보다 훨씬 높고 모든 예측된 bbox를 다사용 한 RetinaNet(99.23%)비견될만 하다. 

Ambiguous Samples 에 대한 성능:

Fig7의 Table 2에서 보면 minival에서 FPN을 사용 하지 않고 feature map $P_{4}$만 사용 할 경우 $ \frac{ambiguous samples}{all positive sample} = 23.16%$이지만 FPN을 사용할 경우 \frac{ambiguous samples}{all positive sample} =7.14%$로 줄어든다(개인 적인 생각은 FPN이 FCOS에서 효과적으로 ambiguous samples문제를 해결한다는 것을 보여주기에 이결과만으로 충분하다고 생각한다..)

이 결과는 저자의 관찰결과(= 대부분의 overlap은 크기 차이가 상단한 object들 사이에 발생하므로 FPN을 사용해 서로 다른 level의 feature map에서 찾게 하면 해결이 가능하다)가 설득력 있다는 근거가 될수 있다.

 저자의 주장에 따르면 overlap이 같은 category에 속한 object들 사이에 일어나는 경우는 ambiguous location에 속한 픽셀(receptive field라고 생각하는게 더 정확할거 같다..)들은 어차피 class label이 같아  overlap에 관여하는 object중 어떤 object를 추정해도 성능 하락에 영향이 없으니 이런 경우를 배제 하면 $ \frac{ambiguous samples}{all positive sample} $은 Fig7의 Table 2의 Amb. samples(diff)(%)의 결과를 얻을 수 있다.(배제 한다는 것은 overlap이 서로 다른 category에 속한 object들에 의해 만들어지는 경우만 고려한다는 뜻이다.)

 이럴 경우 FPN사용시 \frac{ambiguous samples}{all positive sample} =3.75%$ 까지 하락한다.

(추가 적으로 실제 inference할때 ambiguous location에서 생성된 bbox의 비율을 살펴 보면 2.5%의 bbox만이 이 overlapped location에서 생성되었고 그중 서로 다른 category가 overlap된 경우는 1.5%였다고 한다. 즉, 저자가 말하고자 하는 위와 같은 자신의 주장은 타당하나는 것....)

Centerness 의 효용성:

Fig 8 은 centerness를 사용할 때와 그렇지 않을때 의 성능을 보여준다. 직관적으로 알 수 있듯이 결론은 사용하는게 성능 향상에 더 좋다. 다만 $center-ness^{+}$의 경우 center-ness를 Fig 4의 Regression branch 에서 학습 시켰을 경우의 결과 이고, $center-ness$ 는 Fig 4에서 처럼 classification branch에서 학습 시켰을 경우의 결과 이다. 

FCOS vs Anchor based detector:

Fig 9 은 anchor based detector 인 RetinaNet과의 비교이다. 위표는 FCOS와 RetinaNet과의 차이를 최대한 배제한 상태의 실험 결과이다.(FCOS를 설계 할때 기존 RetinaNet에서 사용 하지 않은 Group Normalization(GN)을 사용 하고, FPN을 생성할때 Fig 4에서 $P_{5}$를 사용했는데 RetinaNet에서는 $C_{5}$를 사용해 $P_{6}, P_{7}$을 만들었다는 차이가 있는데 위의 실험 결과는 FCOS에서 GN사용 배제, $P_{6}, P_{7}$ 생성시  $C_{5}$사용등 조건을 최대한 똑같이 맞췄다는 것이다.)

결과는 보는데로 비등하거나 FCOS가 더 좋다. Improvement는 논문 제출 이후 개선한 버전에 대한 결과 값이다. 

 참고로 위 결과를 얻기 위해 FCOS는 RetinaNet을 학습할때 사용했던 Hyperparameter를 그대로 사용했다고 하는데 Hyperparameter는 해당 model에 최적화 해서 사용 하므로 FCOS에 더 잘맞는 hyperparameter를 사용할 경우 성능은 더욱 좋아 질 수 있을 거라고 한다.

(원래 논문에는 region proposal에 사용했을 때 어떤지에 대한 실험도 있는데... 그건 나중에 정리하도록 하자...)

오랜만의 포스팅이다...

읽은 모든 논문에 대해 정리를 하려고 시작했는데..

습관이 덜되고 일에 치이다 보니.. 다시 열심히 해봐야지..

누군가 이 리뷰에서 잘못된 부분을 발견한다면 또는 글쓴이가 잘못 이해하고 있는 부분이 있다고 생각한다면...

주저 없이 댓글을 남겨 준다면 많은 도움이 될거같다.

오늘 리뷰할 논문은 AttendNets이라는 논문으로 DarwinAI 와 Waterloo 대학에서

제안한 내용으로 2020년 9월 archive에 올라왔다.

Title: AttendNets: Tiny Deep Image Recognition Neural Networks for the Edge via Visual Attention Condensers

paper link: https://arxiv.org/pdf/2009.14385.pdf

특징 및 Contribution:

1. 단말 기기에서 image recognition을 수행하기 위한 AttendNets이라는 모델을 제안

2. 단말 기기란 스마트 폰과 같은 기기를 말하며 제안된 모델은 서버의 도움없이 on-device에서 동작할 수 있는 모델이다.

-> 이를 위해 모델 개발시 low-pricision(정확히 말하자면 8bit pricision)이라는 제한 사항을 두었다.

3. Visual Attendtion Condenser(VAC)라는 모듈을 사용하는데 이 모듈은 spatial-channel selective attention을 향상시킨 attention condenser이다. (attention condenser라는 개념이 햇갈렸는데 아래에 이해한대로 열심히 정리해놨다.)

4. 이 모델은 machine-driven design 되었는데 내가 이해한 바가 맞다면 AutoML로 모델 개발했다는 말이다.

구조:

이 모델의 특징적 구조는 visual attention condenser라는 모듈인데 self attention machanism을 사용한 모듈이다.

1. VAC

위 그림은 이 논문에서 주로 사용 되는 self- attention을 위한 구조이다.

이전 까지 타 논문에서 제안되고 사용된 self-attention는 주로 network의 accuracy 향상을 위해 channel-wise attention과 local attention을 분리하고 합쳤던데 반해 이 논문에서는 self-attention machanism을 network 의 효율성 향상을 위한 방향으로 탐구했다.

논문의 필자가 주장하는 바에 따르면 제안된 VAC는 낮은 차원수(reduced dimensionality)의 통합된 embedding을 학습하고 생성 할 수 있는데 생성된 embedding은 channel공간과 spatial 공간의 activation관계를 잘 나타내는 특징을 가진 다고 한다.

VAC는 다음과 같은 하위 컴포넌트로 구성되어있다.

1. Down mixing layer : V'=M(V)

역할: channel reduction

구현 method: point wise convolution

2. Condensation layer: Q=C(V')

역할: 공간도메인에서의 차원 축소(featurea의size축소라고 해석해도 될거 같다) 및 강한 activation결과를 가지는 관심영역(ROI)간의 거리 축소를 통해 spatial attention 응집

구현 method: Max pooling

3. Embedding structure: K=E(Q)

역할: spatial-channel activation 관계의 특징을 내포하는 embedding K 생성

->spatial-channel activation relationship을 characterzing했다고 하는 이유는 down-mixing layer에서 channel 간의

activation 관계를 모델링 하고 condensation layer에서 spatial domain의 activation관계를 모델링 했기 때문인거 같다.

구현 method: grouped convolution, point wise convolution

4. Expansion layer: A=X(K)

역할 : V'에서 관심 영역을 boosting 하기 위한 self-attention value 생성을 위한 spatial domain dimensionality 확대

구현 method: unpooling

5. Selective attention mechanism: V''=F(V', A,S), where S is scale factor

역할: selective attention

구현 method: element wise multiplication

6. Upmixing layer: V'''=M'(V'')

역할: VAC 모듈의 output이 input V와 같은 channel dimensionality를 같게 하기 위한 channel dimensionality 확대

구현 method: point wise convolution

이를 종합해 보면 제안된 VAC모듈의 코드 형태는 다음과 같다고 생각해 볼수 있다.

(어디까지나 수도 코드이다)

down_mixing = torch.nn.Conv2d(in_ch, out_ch,kernel_size=(1,1)) # in_ch > out_ch
condensation_layer =torch.nn.MaxPool2d()
embedding_structure = torch.nn.Sequential(torch.nn.Conv2d(out_ch, out_ch2, kernel_size=(k,k), groups=n),\
        torch.nn.Conv2d(out_ch2, out_ch3, kernel_size=(1,1))) # where k>1, n>1
expansion_layer = torch.nn.MaxUnpool2d()
upmixing_layer = torch.nn.Conv2d(out_ch3, out_ch4, kernel_size=(1,1)) #where out_ch4> out_ch3

V' = down_mixing(V)
Q = condensation_layer(V')
K = embedding_structure(Q)
A = expansion_layer(K)
V'' =V'*A*S #where S is scale factor
V''' = upmixing_layer(V'')

2. Machine-driven Design

논문의 실험에 사용된 모델 구조는 식을 통해 machine-driven된 구조이다.

간단하게 생각하자면 디자인 하고자 하는 모델의 제한사항을 정의한 하고 그 제한 사항을 만족하는 모델을 iterative solving process같은 방식으로 찾는 것이다.

식에서 G(s)는 모델의 생성자이다. 생성된 모델 중 성능평가 함수 U()를 최대화 하면서 동작조건 $l_r(G)=1$ 을 만족하는 모델이 찾고자 하는 모델이다.

$l_r(G)$은 생성된 모델 G가 아래 두 조건을 만족하는지 판단한다.

1. $imagenet_{50}$에 대해 top-1 validation accuracy 가 71% 크거나 같다.

2. 8-bit weight pricision

본 논문에서는 prototype 모델에 대해 아래와 같은 기본적인 정의만 한 상태에서 구체적인 모델의 디자인은 위 수식을 통해 생성한다.

1. input channel=3

2. output logits은 average pooling, fully connected, softmax를 순서대로 거쳐 생성한다.

이렇게 생성된 모델은 아래와 같은 모습이다.

AttendNet-A와 B에서 공통적으로 보이는 특징은 VAC(visual attention condenser)모듈이 모델의 초반부에 집중적으로 사용되고 PEPE(projection-expansion-projection-expansion)모듈이 모델 후반부에 집중적으로 사용된다는 것이다.

PEPE모듈은 machine-driven exploration을 통해 발견한 구조이다.

VAC모듈이 모델 초반부에 많이 사용되는 것은 visual selective attention이 low-mid level visual feature extraction 단계에서 중요한 역할을 한다고 해석 할 수 있다.

AttendNets-A와 B의 구조적 차이는 효율성과 정확성의 균형을 이루며 특정 테스크를 수행하는데 필요한 모델을 찾기 위한 machine-driven exploration의 결이다.

논문의 필자는 이러한 구조적 차이를 macroarchitecture 와 microarchitecture 의 다양성이라고 표현했는데

macroarchitecture의 다양성이란 VAC, PEPE, spatial convolution, point wise convolution등이 서로 다르게 섞여있는 것이고

microarchitecture의 다양성이란 각 VAC, PEPE 모듈 내부의 layer들이 서로 다른 channel수를 갖도록 configuration된것에서 알 수 있다고 주장한다.

(의문은 microarchitecture에 대한 주장은 이해가 가는데, macroarchitecture의 다양성에 대한 주장은 이해가 가지 않는다.

논문에서는 At macroarchitecture level, there is a heterogeneous mix of visual attention condensers, PEPE modules, spatial and pointwise convolutions, and fully-connected layers.

라고 표현했는데 모델 구조를 나타낸 그림에서 AttendNets-A와 B 에서 macroarchitecture level의 차이는 보이지 않는다. 내가 잘못 이해 하고 있는 걸까? )

결과

위 테이블은 $imageNet_{50}$에 대한 대조군과 제안된 AttendNets 의 실험 결과를 보여준다.

AttendNets은 대조군들에 비해 낮은 8-bits weight pricision과 적은 MACs을 가짐에도 불구하고

대조군들과 유사하거나 높은 Top-1 accuracy를 보여준다.

목표했던 단말에서 on-device로 동작 가능한 model을 제안한다는 주장에 힘을 실어 주는 결과로 보인다.

빠른 구조의 네트워크를 찾던 중 아래 논문을 보게 되어 정리하고자 한다.

centernet 이란 이름의 논문이 두개 있어서 헷갈릴 수 있는데 여기서 리뷰하는 논문은 아래 논문이다.

title: Objects as points (2019년 아카이브에 올라왔다.)

paper link: arxiv.org/pdf/1904.07850.pdf

code link: github.com/xingyizhou/CenterNet

centernet의 특징

• One-stage detector
  어찌 보면 당연하게도 centernet은 YOLO, SSD 등과 같은 one-stage detector이다.
  다만, YOLO나 SSD가 미리 정해진 anchor에서 bounding box의 overlap을 기준으로 삼는것과 달리
  centernet은 각 object에 대해 단 하나의 중심점을 key point estimation방식으로 추정한다.
  
  
• Object detection 문제를 key point estimation문제로 정의해 풀었다.
  바로 위의 설명과 겹치는 부분이 많지만 기존 one-stage detector 들은 각 anchor 위치에서 정해진 비율의 bbox들에 대해
  overlap 정도를 기준으로 학습하지만 centernet은 feature map으로 부터 각 object의 center 위치를 확률 맵으로 나타내어 학습한다. center 위치를 key point로 정의하고 문제를 푼 것이다. 
  

• 구조가 매우 단순해 이해 하기 쉽고 orientation, pose, 3d bbox 추정으로 쉽게 확장 가능 할 것같다.

구조

수치는 input: 3x256x512, output stride: 4 기준이다. 

• 위 centernet 구조 그림에서 처럼 centernet은 feature를 생성하는 backbone과 3개의 header로 이루어져 있다.
  
  
• 해더는 각각 center heatmap, center offset, width and height 를 출력한다. 
  
  
• center heatmap은 channel index가 각 object category에 해당한다. 예를 들어 사람의 object id=0 이면
  centerHeatmap[0,:,:]에는 사람의 center 위치에 해당하는 pixel의 값이 1에 가까울 것이다. 
  (그림에서 center heatmap 위의 ncls x 64 X128은 출력 텐서의 모양이고 ncls는 number of classes의 약자이다.)
  
  
• center offset은 output stride때문에 발생하는 discretization error를 보상하기 위해 추정하는 것으로 각 object center 위치를
  input image scale로 해석할때 오차를 보상하기 위한 값이다. 예를 들어 input image에서 A 라는 object의 center가 (146, 133)에 
  위치한다면 출력 center heatmap 텐서에서 해당 object의 위치는 (36,33)이다. 하지만 실제 (146/4, 133/4)=(36.5, 33.25)이므로
  (0.5, 0.25)의 오차가 발생한다. 이 오차가 output stride에 의해 발생하는 discretization error 이고 이를 보상해 주기 위해 추정한다.
• 마지막으로 width and height 텐서는 object의 width, height를 추정 하는 텐서이다. 예를 들어 object id =0 인 물체에의 width, height는 widthAndHeight[0:2, x,y] 위치의 값이고 object id=4인 물체의 width, height는 widthAndHeight[8:10,x,y] 위치에 저장된다.

Loss

• center heatmap loss

$Y_{xyc}$=1은 object center 위치의 GT 값이다. 학습 초반 $\hat{Y}_{xyc}$의 값이 작다면 $(1-\hat{Y}_{xyc})^{\alpha}$ 의 값이 상대적으로 커서 loss 가 커지고 학습 후반으로 갈록 $\hat{Y}_{xyc}$의 값이 0에 가까워 지면 $(1-\hat{Y}_{xyc})^{\alpha}$ 의 값이 기하 급수적으로 작아져 loss에 거의 영향을 미치지 않는다. 

반대로 center point가 아닌 위치에서 학습 초반에 $\hat{Y}_{xyc}$ 의 값이 크다면 $(1- Y_{xyc})^{\beta} (\hat{Y}_{xyc})^{\alpha}$의 값이 상대적으로 커서 loss에 영향을 크게 미치지만 학습 후반 부로 갈수록 이 값이 기하 급수적으로 작아져 loss가 줄어 든다.

• center offset loss 

구조 설명에서 언급한것 처럼 output stride로 인해 발생하는 discretization error를 보상하기 위해 추정하는 offset값이다. 

$\frac{p}{R}-\tilde{p}$ 부분이 의미하는 것이 discretization error 이고 여기서 R은 output stride를 의미한다. 

p는 input image scale에서 object center의 x 또는 y 좌표 이고 $\tilde{p}$ 는 소수를 버림한 $\frac{p}{R}$ 값이다.

이 loss는 위와 같이 단순히 L1 loss를 이용한다.

• width and height loss
  

width 와 height loss는 단순히 L1 loss 를 이용 하여 위와 같이 구한다. 

• total loss
  

total loss는 위와 같고 논문에서는 $\lambda_{size}$ =0.1 , $\lambda_{off}$=1 로 설정했다.

이 정리만 봐선 내용 파악이 힘들것 같아 근시일 내에 GT 만드는 내용도 추가해서 정리 해야 할것 같다.....