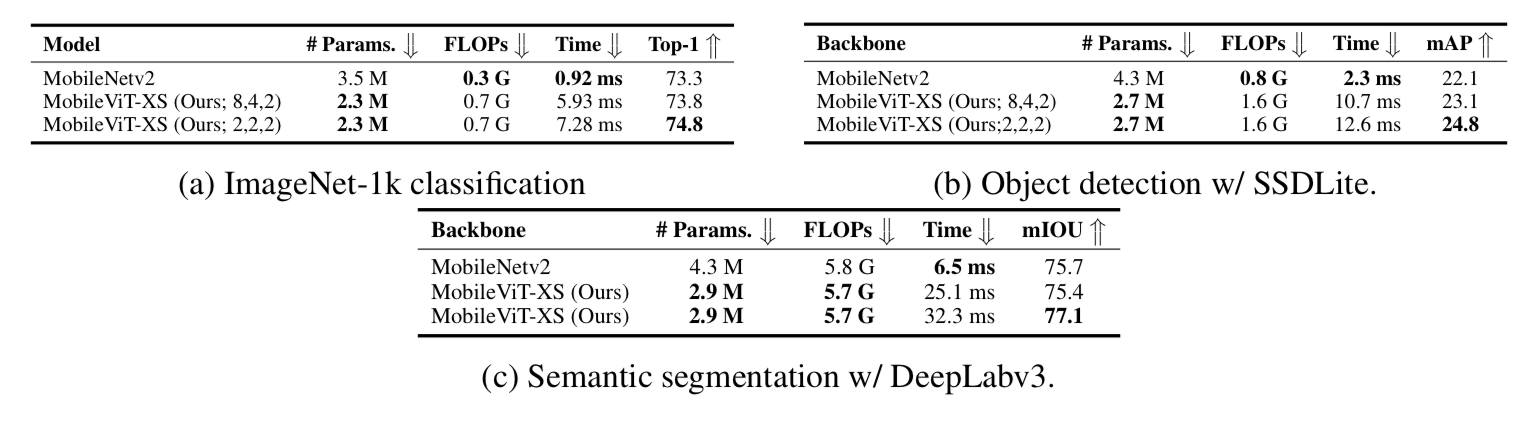
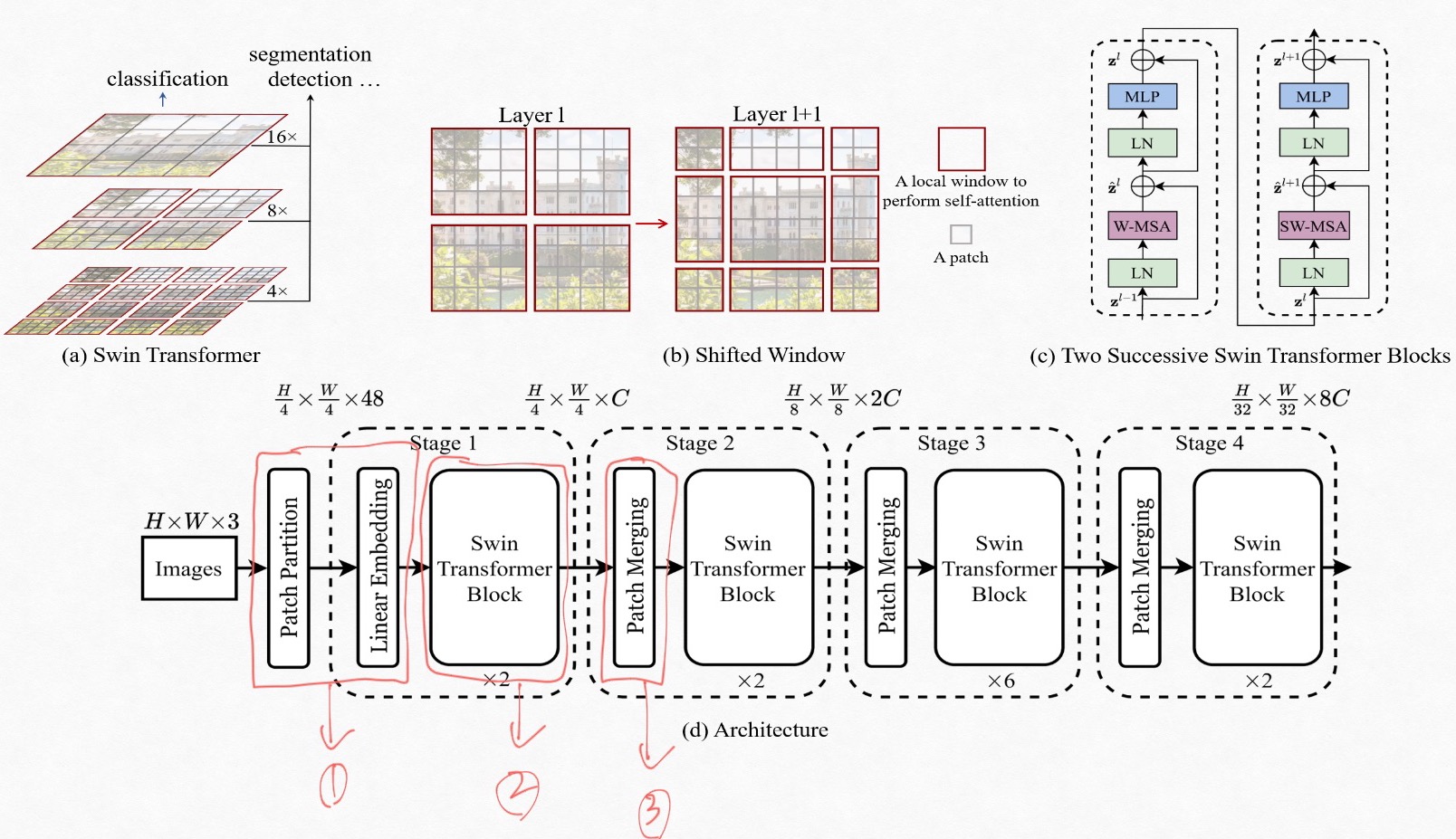
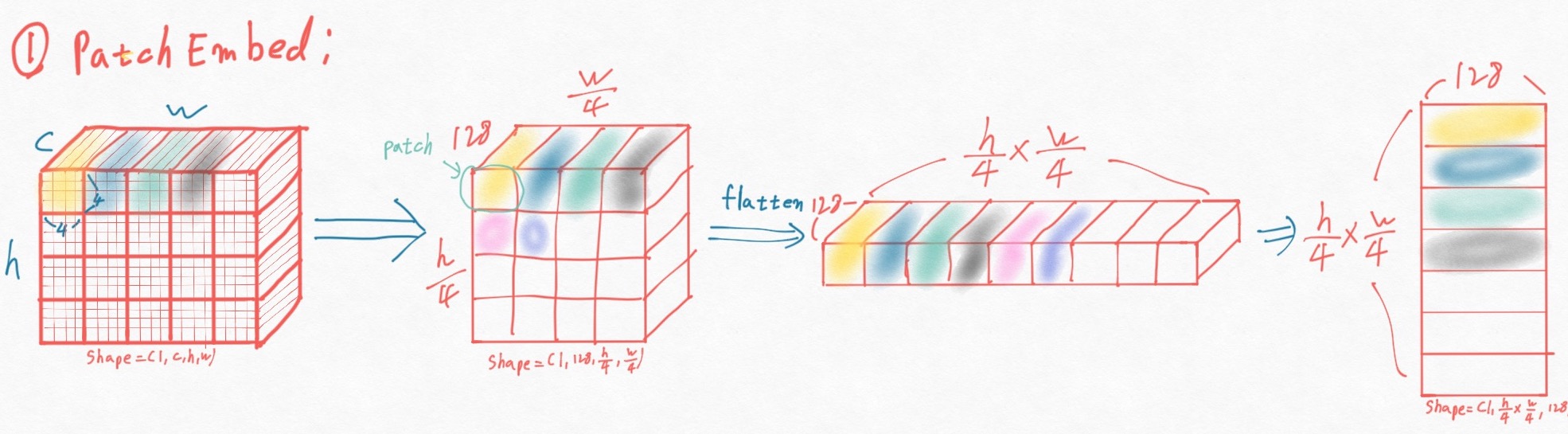
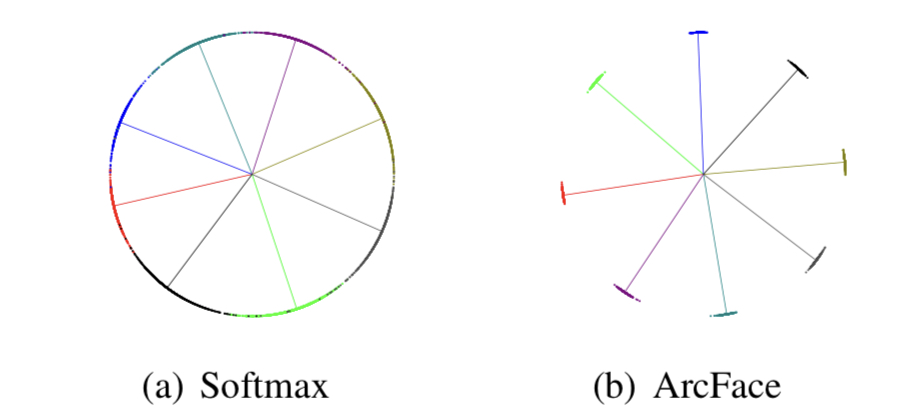
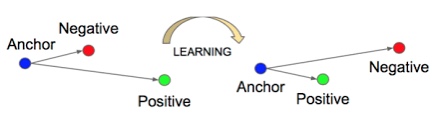
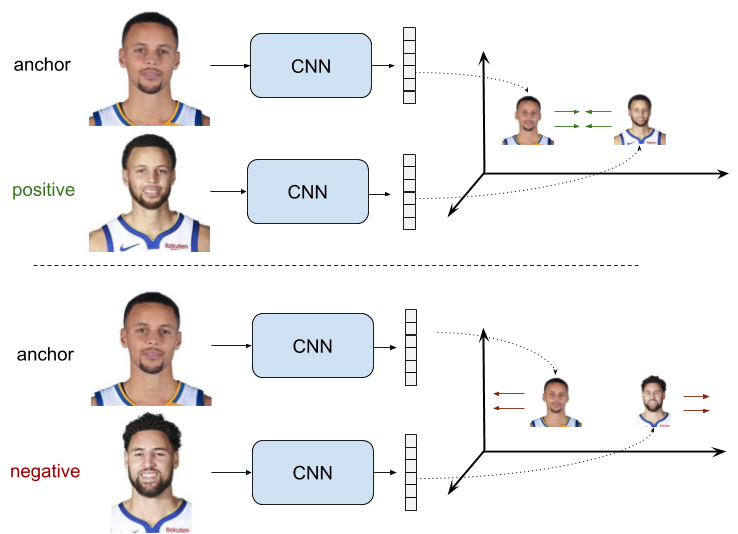
이 논문은 새로운 방식의 bbox regression 방식인 DFL(distribution focal loss) 와 localization quality와 classification score 동시에 표현해 최적화 하는 quality focal loss를 제안하고 이 둘을 합쳐 Generalized Focal loss라고 명명한다.
localization quality란 FCOS 관점에서 보면 object의 centerness score에 해당한다.
Tile: Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
One-stage detector basically formulates object detection as dense classification and localization. The classification is usually optimized by Focal Loss and the box location is commonly learned under Dirac delta distribution. A recent trend for one-stage d
arxiv.org
git:https://github.com/implus/GFocal/blob/master/mmdet/models/losses/gfocal_loss.py
기존 방식의 문제점:
문제 1. 학습/추론 시 localization quality estimation 과 classification score 의 사용 방식이 불일치
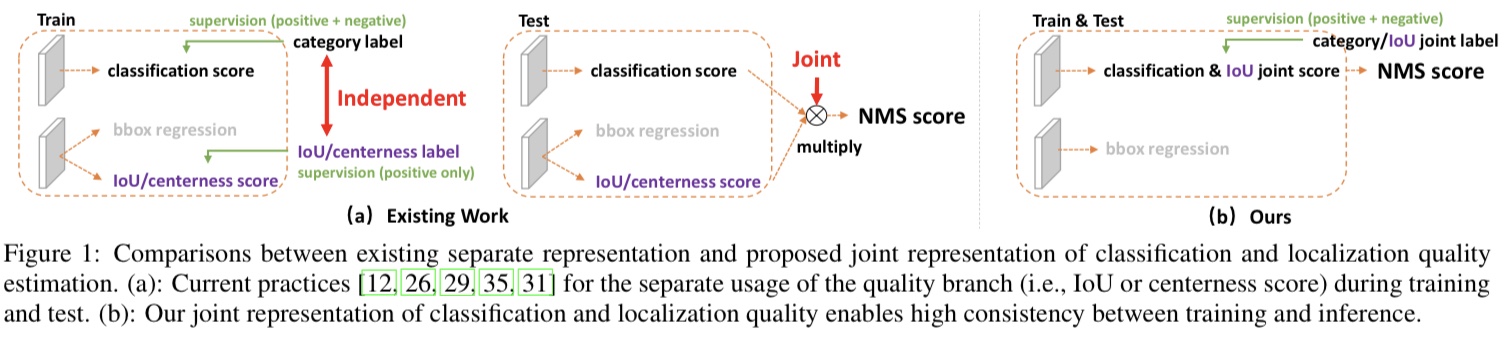
사유 1. FCOS 같은 one stage detector들은 학습시 classification score 와 centerness(또는 iou)score 가 별개로 학습되지만 inference 시에는 nms전에 두 score를 join해서 사용(element wise multiplication)한다. 위 Figure 1의 (a)의 train와 test이 이를 잘 보여준다.
사유 2. positive sample 위치에만 localization quality estimation에 대한 label이 주어진다. 학습과 추론 단계에서의 두 score의 학습/사용 방식이 상이한 점이 성능 저하로 이어 질 수 있음
문제 2. 박스 표현의 경직성(Inflexible representation of bouding boxes)
기존 방식들은 positive sample 위치에만 box gt를 할당해 regression 하는 방식을 취하는데 이는 dirac delta distribution으로 볼 수 있다. 이유는 이런 단순 한 box gt 할당은 database에 존재 할 수 있는 다양한 애매하고 불명확한 상황을 고려하지 못하기 때문이다. 예를 들어 물체의 occlusion, shadow, blur등으로 인해 물체의 경계가 불분명 해 질 수 있고 이 경우 Dirac delta distribution은 이런 경우를 커버하기엔 제한 적이다.

위 Figure 3에서 보면 이 논문에서 제안하는 방식으로 bbox 표현을 학습 하면 가림, 그림자, 흐림 등의 경우에도 target 물체의 모양을 고려해 더 fit한 bbox를 추측 할 수 있다는 것을 나타낸다. 왼쪽 그림의 경우 서핑 보드가 파도에 의해 가림이 생겼는데 이 논문에서 제안한 방식으로 학습한 경우 녹색과 같이 박스가 추측 된다.
이미지 오른 쪽의 그래프는 아직 이해 하지 못해도 된다. 이것 distribution focal loss파트를 읽어 보면 이해 되는 그래프이다.
몇몇 논문에서 bbox를 gaussian distribution으로 표현해 학습 하는 방법을 제안했지만 이는 단순 한형태여서 다양한 상황을 커버하지 못한다(고 주장한다)
Method

Quality Focal Loss(QFL)
quality focal loss는 localization quality estimation과 classification score를 혼합한 classification-iou score를 최적화 하기 위한 loss function으로 위 “기존 방식의 문제점” 섹션에서 언급한 문제 1의 train-test inconsistency를 해결한다.
localization quality estimation과 classification score를 혼합했기 때문에 one-hot category label이 아닌 soften된 label $y \in [0,1]$ 이 사용된다. $y=0$은 negative sample로 0 quality score(IoU score) 를 나타내고, $ 0 < y \leq 1 $ 은 positive sample로 quality score y가 loss의 target y로 사용된다.
여기서 localization quality estimation과 classification score를 혼합하면 왜 one-hot category label 이 아니라 soften된 label 이 target이 되는지 의문이 들 수 있다. 나도 처음엔 이게 의문이었다. 이유는 classification score(one-hot)에 각 positive sample의 위치 anchor(또는 center position)에 해당하는 pixel에서 추론된 predicted bbox와 target bbox의 IoU score를 곱해서 target으로 사용 하기 때문이다. (one-hot label에서 positive sample의 label은 1이니까 IoU score곱한다는 의미는 IoUscore를 target label로 사용하겠다는 것과 같다). 이게 위 Figure 4의 existing work 과 GFL의 차이에서 label이 soften된다고 나타낸 이유이다.
QFL의 수식은 아래와 같다.
$$QFL(\sigma) = -\left \vert y - \sigma \right \vert ^{\beta} ((1-y)\log{(1-\sigma)} + y\log{\sigma}$$
focal loss에서 달라진 부분은 두 부분이다.
1. cross entropy part인 $-\log{(p_t)}$ 가 binary classification의 complete form인 $1((1-y)\log{(1-\sigma)}+y\log{\sigma}$ 로 바뀌었다.
2. scaling factor $(1-p_t)^gamma$ 가 추정치 $\sigma$와 label $y$의 L1 distance $\left \vert y - \sigma \right \vert ^ \beta$ 로 바뀌었다.
위 형태에서 $y=\sigma$일 때 global minimum을 갖는다.
multi-class classification의 경우 sigmoid를 이용해 multiple binary classification으로 문제를 정의 한다. multiple binary classification에서 각각의 binary classification을 위와 같은 방식으로 풀면되므로 어려울 건 없다.
코드는 아래와 같고 mmdetection 에서 가져왔다. 필요 한 부분에 주석을 달아 두었으니 위 내용과 비교하며 보자.
def quality_focal_loss(
pred, # (n, 80)
label, # (n) 0, 1-80: 0 is neg, 1-80 is positive
score, # (n) reg target 0-1, only positive is good
weight=None,
beta=2.0,
reduction='mean',
avg_factor=None):
# all goes to 0
pred_sigmoid = pred.sigmoid()
pt = pred_sigmoid
zerolabel = pt.new_zeros(pred.shape)
# 아래는 negative sample 에 대한 loss
loss = F.binary_cross_entropy_with_logits(
pred, zerolabel, reduction='none') * pt.pow(beta)
label = label - 1
pos = (label >= 0).nonzero().squeeze(1)
a = pos
b = label[pos].long()
# positive goes to bbox quality
pt = score[a] - pred_sigmoid[a, b]
# positive sample 에 대한 loss 이고 target 으로 사용 되는 score 는 이 논문에서 제안한
# iou 와 classification score 를 결합하여 soften 한 label 이다.
loss[a,b] = F.binary_cross_entropy_with_logits(
pred[a,b], score[a], reduction='none') * pt.pow(beta)
loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
return lossDistribution Focal Loss
DFL은 참신 하면서도 이해가기 매우 쉽다. DFL에 대하 설명 하기 전에 이 논문에서 bbox regression문제를 어떻게 정의 했는지 먼저 살펴보자. 이 부분이 꽤 참신하며 yolo등에서 bbox regression에 이 방식을 채용했다.
이 논문은 anchor 또는 center point위치 로 부터 bbox의 각 변까지의 거리를 regression으로 직접 추론 하는 방식 대신 기대값을 구하기 위한 distribution을 추론 하는 방식으로 문제를 변경했다. 기존 bbox 추론 네트워크 들은 대부분 object 중심에 해당하는 anchor 에서 bbox의 각 변까지의 거리 (l,t,r,b)(아래 그림 참조) 에 해당 하는 4가지 값 scalar를 직접 추론 하는 방식을 채택했다. 이 방식을 굳이 수식으로 나타내면 특정 값에서만 확률 이 1인 Dirac delta function으로 나타낼 수 있기 때문에 이 논문에서는 기존 방식들은 distribution을 dirac delta로 가정 하고 문제를 풀었다고 말한다.

이 논문은 l,t,r,b를 직접적으로 추존 하는 대신 l,t,r,b의 확률 분포를 추론하고 이를 이용해 기대값을 계산함으로써 최종 l,t,r,b를 계산 한다. 수식으로 보면 아래와 같다.
$$\hat{y} = \sigma_{i=0}^{n}P(y_{i})y_{i} $$
위 식에서 $y_{i}$는 각변 까지의 거리 l,t,r,b의 discrete 한 값이고 $P(y_{i})$는 네트워크가 추론한 현 anchor에서 object boundary 까지의 거리 l,t,r,b가 $y_{i}$일 확률 값이다.
좀더 구체 적으로 예를 들자면 DFL은 object boundary 까지의 거리를 직접적으로 추론하는 것이 아니라 anchor 로 부터 object의 왼쪽 경계 까지 거리 $l$이 1일 확률 0.01, 2일 확률 0.05, 3일 확률 0.06, … 8일 확률 0.5, 9일 확률 0.2, … 16일 확률 0.01 이니까 $l$의 기대값은 XX이다! 라고 추론하고 이 기대값이 최종 추론 값이다.
여기서 당연한 의문이 생길 수 있는데 “확률 분포는 그렇다 치고 $P(y)$ 를 구해서 기대값은 구하려면 $y$를 당연히 알아야 하는데 이건 어떻게 구했나?” 가 그 의문이다.
논문의 저자들은 coco trainval135k 데이터 셋에서 bbox regression target $l,t,r,b$의 histogram을 구했다. 그 결과가 아래 histogram 이다. 이를 보면 x축인 regression target이 약 1~16까지 분포해 있는 것을 알 수 있다.
이 정보에 기반해 $ y \in [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]$ 으로 미리 정해 놓고 각 $y_{i}$가 현 anchor에 대응 하는 각 변까지의 거리일 확률 분포 $P(y_{i})$를 추론 하도록 했다.

이러한 확률 분포 $P(y)$를 fitting 하기 위해 이 논문은 DFL(distribution focal loss)를 제안 하는데 아주 간단하고 명확해 보인다. 식은 아래와 같다.
$$DFL(S_{i}, S_{i+1}) = -((y_{i+1}-y)\log(S_{i}) + (y-y_{i})\log(S_{i+1}))$$
target 을 y라 할때 y와 가장 가까운 값 $y_{i} \leq y \ge y_{i+1}$ 인 $y_{i}, y_{i+1}$에서 $P(y)$가 peak 값을 가지도록 위와 같은 complete form의 cross entropy 를 이용해 학습 한다. $S_{i}=\frac{y_{i+1}-y}{y_{i+1}-y_{i}}, S_{i+1} = \frac{y-y_{i}}{y_{i+1}-y_{i}} $ 이다. ($S_{i},S_{i+1}$ 이 왜 저렇게 되는지 궁금하면 linear interpolation을 생각해 보자)
예를 들어 실례를 들어 보자면 unnormalized logits
$ y_{i}=[9.38, 9.29, 4.48, 2.55, 1.30, 0.42, 0.03, -0.28, -0.51, 0.83, -1.27, -1.56, -1.78, -1.94, -.193, -1.38]$ 이라고 할때 target $y=0$ 이면 cross entropy 에 의해 $p(y_{0}), p(y_{1})$이 근처에서 peak 값을 갖도록 학습이 되는 방식이다.
코드로는 아래와 같다. 코드는 공식 mmdetection 에 삽입된 코드를 가져왔다.
def distribution_focal_loss(
pred, #normalized 되지 않은 y prediction 값이다. 즉 softmax 씌우기 전의 값
label, # target label 이다.
weight=None,
reduction='mean',
avg_factor=None):
disl = label.long()
disr = disl + 1
wl = disr.float() - label # y_{i} 에 대한 weight 계산
wr = label - disl.float() # y_{i+1} 에 대한 weight 계산
loss = F.cross_entropy(pred, disl, reduction='none') * wl \
+ F.cross_entropy(pred, disr, reduction='none') * wr
loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
return loss
결과

이 논문에서 제안한 QFL, DFL의 효과에 대한 결과 이다. DFL보다는 QFL이 더 직접적으로 AP 향상에 영향을 미치는 것 처럼 보인다. QFL 만 적용 했을때가 DFL만 적용 했을때 보다 AP 컷다. 둘 모두 사용 하면 둘중 하나만 썻을 때 보다 AP 것을 알 수 있다.
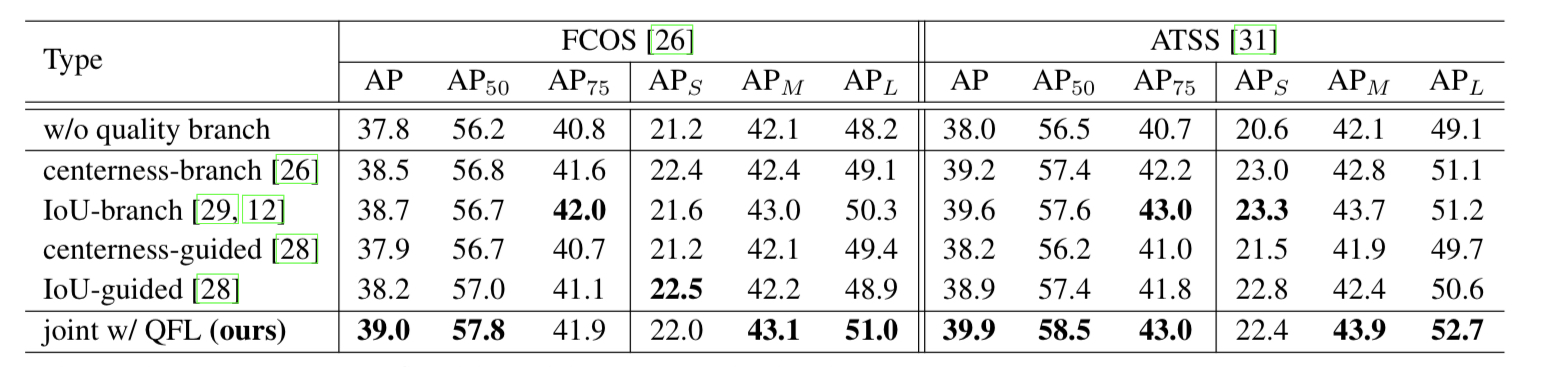
fcos와 atss에 QFL을 적용한 결과 전반적인 성능향상을 보이는 것을 알 수 있다

DFL도 적용시 전반적으로 성능향상을 이끌어 낸다늩 것을 알 수 있다
참조: mmdetection 및 논문 원문
-끝-
'Deeplearning > Loss' 카테고리의 다른 글
| [metric loss] additive angular margin loss (0) | 2021.11.26 |
|---|---|
| [Metric learning loss] Triplet loss 설명 (0) | 2021.11.24 |