[metric loss] additive angular margin loss

additive Angular margin loss

Additive angular margin loss 는 metric learning에서 사용하는 loss로 ArcFace라는 논문에서 face recognition문제를 해결하기 위해 제안했다. 얼굴인식 문제를 풀기위해 제안되었을 뿐 similarity 문제를 푸는 대부분에 응용이 가능 하다.

목표는 triplet loss와 유사하게 (동작 방식은 전혀 다르다 목표만 유사하다) intra-loss는 감소 시켜 같은 클래스에 속한 입력들이 feature space에서 응집력을 가지게 학습시키고 inter-loss는 크게 해서 서로 다른 클래스에 속한 입력들은 feature space에서 구분가능한 만큼 떨어지게 학습시키는 것이다.
단 additive angular margin loss에서 의 거리는 Euclidian 거리가 아니라 loss의 이름에서 유추 가능 하듯 angular 거리 즉 각도의 차 이다.  (왜 각도 차 인지 아래  '개념' 섹션을 참조하면 이해에 도움이 될 것 이다.)

- intra-loss: 같은 클래스에 속한 입력의 feature 들 간의 loss
- inter-loss: 다른 클래스에 속한 입력의 feature 들 간의 loss

장점

softmax나 triplets loss 는 다음과 같은 문제를 가지고 있다.
1. softmax의 문제
- 분류해야하는 클래스의 개수가 증가 할 수록 fc 레이어의 아웃풋의 크기가 선형 증가 하게 되어있다.
- 학습된 feature는 Closed-set(폐쇄형) 분류 문제에는 충분할 수 있지만 Open-set(개방형) 얼굴 인식 문제에 충분한 분별력을 갖지 못한다.(이건 논문에 써있는데 얼굴 인식 문제를 직접 풀어 본적이 없어서 실제로 그런지는 잘 모르겠다. )
2. triplets loss의 문제
- triplets loss를 설명 할때 [주의사항]으로 써놓았는데 triplets은 (anchor, positive, negative) 3쌍의 sample이 필요하다. 입력의 class가 커지면 저 3쌍의 결합 개수는 폭발적으로 증가 할 수 있다.
- semi-hard triplets 를 선택하는게 굉장히 힘들고 비용 소모가 크다.

고로 장점은
triplets loss 처럼 semi-hard 한 샘플을 신중하게 선택할 필요가 없으며 softmax 보다 더 분별력있는 feature를 학습 할수 있게 해준다.
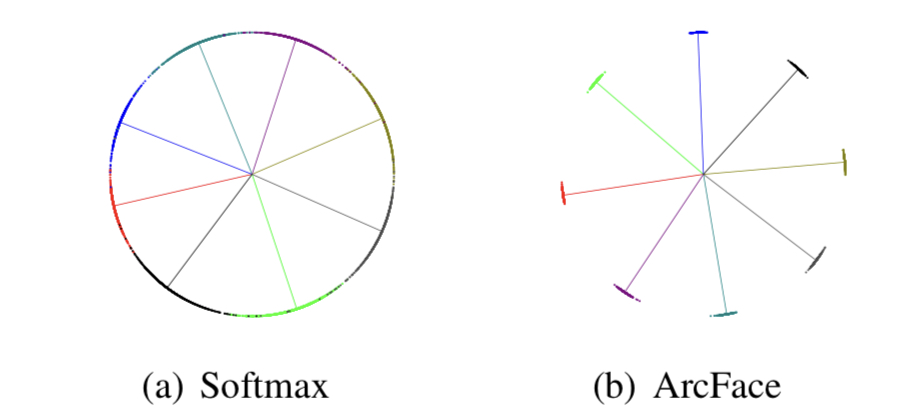
아래 그림은 softmax와 additive angular margin loss를 이용해 학습한 feature를 2D 공간에 그린것이다.
이렇게 보면 softmax보다 additive angular margin loss가 훨씬 decision boundary가 명확해 보인다.

Fig 1. (좌) softmax를 이용해 학습한 feature의 2상에서의 분포, (우) additive angular margin loss를 이용해 학습한 feature의 2d 상에서의 분포

연산

Fig 2. additive angular margin loss 

위 그림은 additive angular margin loss가 어떻게 동작하는지 보여준다.

classification 문제를 기준으로 설명 하자면 대부분의 DCNN(Deep Convolutional Neural Networks)모델의 마지막 레이어는 FC(fully connected) layer이다.
이 FC layer의 출력을 feature 라고 하고 기호로 $x$라 하자. (위 그림의 $x_i$가 바로 이 feature이다.)

$x \in R^d$  _($x$가 d차원 상에 있다면)_ 라 하고 $W \in R^{dxn}$ 이라 하자.  여기서 $n$ 은 클래스의 개수 이다. (아래 저차원에서의 예를 들어 다시 설명할 것이다.)
additive angular margin loss 의 입력으로 들어온 $x_i$는 normalization 된 후
normalization 된 W와 메트릭스 곱 $W^Tx$연산을 한다.
우리는 $W^Tx$ 연산을 $W$의 각 column에 해당하는 $w_j$ $j \in (1, ..., n)$ 벡터와 입력 $x$ 벡터의 내적 연산 즉 $$w_j \cdot x$$으로 해석 할 수 있다. ($w_j$ 가 $W$의 column 벡터 이므로 $R^d$ 상에 존재 하며 $x$와 차원이 같으므로 내적이 가능하다.)

내적연산이 $\vec{a} \cdot \vec{b}= |\vec{a}||\vec{b}|\cos\theta$ 임을 떠올려 보자.

우리의 상황에 적용하면 아래와 같이 된다.
$$\vec{w_i}\cdot\vec{x}= |\vec{w_j}||\vec{x}|\cos\theta$$
여기서 $w_i$, $x$는 normalization 된상태 이니 $|\vec{w_i}|=1$, $|/vec{x}|=1$ 이다. 즉, $w_j  \cdot x=\cos\theta$ 이다.

$w_j  \cdot x=\cos\theta$ 의 값을 $acos$에 대입하면 $\theta$를 구할 수 있다. 이 $\theta$에 $margin$을 더해 주고

scale $s$를 곱하면! 위 그림 Fig2 의 별표 펴진 $s*\cos(\theta+m)$ 이 구해진다. 

이렇게 구한 값을 원래의 softmax의 입력으로 넣으면 additive angular margin loss가 완성고 아래와 같이 정리 할 수 있다. 

$$L = -\frac{1}{N}\sum_{i=1}^{n} \log \frac{e^{s*\cos \theta_{y_{i}}}}{e^{s*\cos \theta_{y_{i}}}+\sum_{j=1,j \neq y_{i}}^{n}}$$

 

개념

additive angular margin loss 가 동작 하는 기본 개념은 각도 차이이다. 

고차원은 어려우니 저차원에서 예를 들어 보자.

입력을 아래와 같다고 하자. $$x=(1,2,3)$$, $$W_{3,2}=\begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 &6 \end{pmatrix}$$ 

노멀라이제이션 하면 아래와 같이 된다. ($W$ 매트릭스는 column 축으로 normalization한다.)

$$ x=(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}})$$

$$W_{3,2}=\begin{bmatrix} \frac{1}{\sqrt{14}}& \frac{4}{\sqrt{77}} \\\frac{2}{\sqrt{14}} &\frac{4}{\sqrt{77}} \\\frac{3}{\sqrt{14}} &\frac{4}{\sqrt{77}}\end{bmatrix}$$ 

 

두 입력을 선형 연산 하면 

$$W^{T}x= \begin{bmatrix} a &\\ b \end{bmatrix}$$

가 되고 a,b는 normalization 되었으니 그 크리 $|a|, |b|$ 는 1이다. (a,b 는 $W^Tx 의 결과를 나타내는 두 값이다. 수식을 다 쓰기 힘들어 저렇게 간단하게 표현했을 뿐이다.)

그때 $W$의 각 column vector (1,2,3), (4,5,6) 각각을 3차원 공간 상에서 2개 클래스의 feature의 centre 좌표로의 벡터로 본다면

입력의 feature인 $x$와 $W$의 columnd 벡터들의 내적은 각 클래스를 대표하는 feature 벡터와 입력의 feature가 이루는 각이 얼마나 작은가? 를 알아 보는 과정으로 해석 할 수 있다. 

 

각 클래스의 대표 벡터인 $W$의 column 벡터들과 $x$ 가 모두 normalization 되어있으니 그들의 magnitude는 모두 1로 같으므로

각도 (angular)의 차이만 보겠다는 뜻이다.

기하적으로 해석하면 magnitude가 모두 1이므로 각 클래스의 대표 feature 벡터 와 입력의 feature 벡터 모두 이 예에서는 3차원 공간에서 구의 표면에 위치하고 addtive angular margin loss 는 이 구의 표면 위에서 같은 클래스에 속하는 feature 벡터들이 구의 표면 상에서 서로 가까운 위치에 놓이도록 벡터간의 각도를 작게 한다는 개념이다.