[Metric learning loss] Triplet loss 설명

Metric learning loss

Metric learning 은 데이터간의 유사도를 잘 수치화 하는 거리 함수(metric fucntion)을 학습 하는 것이다.

Metric learning loss는 입력으로 부터 추출된 feature들 간 상대적 거리를 추정하기 위한 loss로 명시적인 목표 값이 주어지고 해당 목표값 추정을 목적으로 하는 cross entropy나 regression loss와 개념이 다르다.

Detection이나 segmentation에 흔히 쓰이지는 않지만 간단하게 말하면
같은 클래스에 속한 입력간의 거리는 가깝게 만들고 하고 다른 클래스에 속한 입력간의 거리는 최대화 할때 씌인다. instance segmentation에서 같은 클래스의 서로 다른 instance를 분리 할때 유사한 개념이 사용되기도 한다.

face identification, few shot learning,  recommendation  등에 사용할 수 있다.

널리 알려진 것중 이 포스트 에서 알아 볼건 triplets loss 이다.

 

triplets loss

Fig 1. Triplet loss의 개념

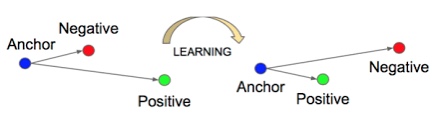
triplets loss는 $R^k$ 에서(k는 feature의 dimension)  같은 클래스 또는 특정한 기준에서 유사한 입력 사이의 거리를 가깝게 하고 서로 다른 클래스, 유사하지 않은 입력 사이의 거리를 멀게 만드는데 목적이 있다.  Fig 1. 에서 Anchor는 기준이 되는 입력이고
Negative는 입력과 다른 클래스 , Positive는 입력과 같은 클래스이다.

 

그림에서 알 수 있듯이 LEARNING 하고 난 후 Anchor,Positive sample사이의 거리는 가까워 졌고 Anchor, Negative sample 사이의 거리는 멀어 졌다.

 

입력이 이미지 일때를 기준으로 예를 들어 보자.

Fig 2. Triplet loss의 예

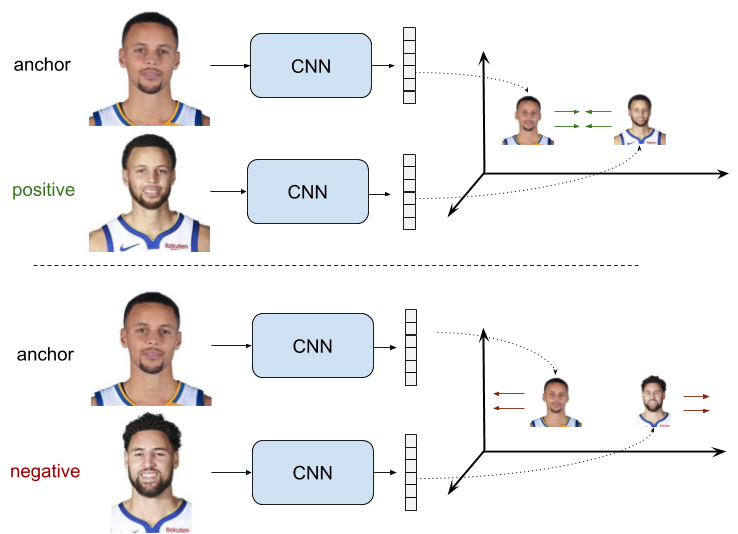
위 그림에서 입력을 얼굴 사진들을 $x_a$, $x_p$, $x_n$ 이라 했을 때
- $x_a$, $x_p$ 는 서로 같은 사람의 얼굴, 즉 같은 클래스
- $x_a$,$x_n$ 은 서로 다른 사람의 얼굴, 즉 다른 클래스
이다.

여기서 $x_p$, $x_n$을 $x_a$ 를 기준으로 같은 클래스, 다른 클래스로 구분을 했는데
이렇게 기준이 되는 입력을 anchor라고 표현하고 anchor 같은 클래스면 positive sample
anchor와 다른 클래스 이면 negative sample이라 한다.
(입력 $x$의 아래 첨자가 $a,p,n$인 이유가 anchor, positive, negative 의 앞 글자를 딴것이다. )

$d(x_i,x_j)$ 를 $R^k$ 에서의 $x_i$, $x_j$ 사이의 거리라 할때  triplet loss의 목적은 아래와 같다. 
- $d(x_a, x_p)$는 최소화
- $d(x_a, x_n)$는 최대화

이때 단순히 최대화 하는것은 목적이 불분명하니 특정한 기준 $\alpha$을 도입해
같은 클래스 간의 거리보다 서로 다른 클래스간의 거리가 $\alpha$ 만큼 크도록 수식을 구성하면 아래 식과 같다.
$$d(x_a, x_n) > d(x_a, x_p)+ \alpha     $$

위 수식은 $$ L(x_a, x_p, x_n) = d(x_a, x_p) -d(x_a, x_n) + \alpha $$ 으로 다시쓸 수 있는데
$d(x_a, x_n)$ 이 커져서 위 수식이 0이하가 되면 그로 부터 network가 배울 필요가 없으니
$$ max(0, d(x_a, x_p) -d(x_a, x_n) + \alpha)$$ 으로 사용한다.

 

triplet loss를 사용할때 주의 할점

이 로스는 $x_a, x_p, x_n$ 의 3쌍이 필요한데 이 3개의 쌍을 어떻게 선택하느냐에 따라 학습의 안정성과 성능이 달라질 수 있다.
$d(x_a, x_p)$ 가 너무 작은 쌍이 dataset의 대부분을 이루고 있다면 여기서 배우는 정보량이 너무 적을수 있고 $d(x_a, x_n)$가 이미 이미 $margin$ 역할을 하는 $\alpha$보다 크면 이런 샘플에서도 학습할 정보량이 부족하다.
특히 negative sample의 선택이 중요하다고 보는 경우가 많다.
negative sample에 따라
* Easy Triplets: $d(x_a, x_n) > d(x_a, x_p)+\ alpha$ 인 경우
* Hard Triplets: $d(x_a, x_n) < d(x_a, x_p) $ 인 경우
* Semi-Hard Triplets:$ d(x_a, x_p) < d(x_a, x_n) < d(x_a, x_p) +\alpha$ 인 경우
로 나누기도 한다.

거리를 계산하는 함수 $d(x_i, x_j)$는 Euclidian 등 원하는 방식을 선택하면 된다.

 

참조

pytorch에 torch.nn.TripletMarginLoss 가 있지만
$(x_a, x_p, x_n)$ 샘플을 자동으로 선택해주는 기능은 없는 것으로 보인다.