오늘 정리할 논문은 swin transformer로 요즘( 혹은 한동안) 핫한 transformer를 비전 테스크에 적용한 논문이다.
기존 CNN 기반의 backbone을 사용하지 않고 순수하게 transformer를 이용해 feature를 이미지에서 feature를 뽑아 낼 수 있다는 것을 보여준다.
Title :
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
This paper presents a new vision Transformer, called Swin Transformer, that capably serves as a general-purpose backbone for computer vision. Challenges in adapting Transformer from language to vision arise from differences between the two domains, such as
arxiv.org
GitHub - microsoft/Swin-Transformer: This is an official implementation for "Swin Transformer: Hierarchical Vision Transformer u
This is an official implementation for "Swin Transformer: Hierarchical Vision Transformer using Shifted Windows". - GitHub - microsoft/Swin-Transformer: This is an official implementation...
github.com
Contribution
Transformer는 NLP분야에서 LSTM을 대체 할 수 있는 방식으로 연구되다 비전쪽에서도 다양한 문제에 응용되고 있다.
하지만 텍스트와 영상은 그 특성이 서로 다르다. 구체 적으로 영상에 transformer를 적용하는 것에는 다음과 같은 문제를 해결해야 한다고 이 논문에서는 말하고 있고, 각각에 대한 본인들만의 해결책을 재시 했다.
1. word token과 달리 visual element는 scale이 다양하다.
NLP를 정확히 몰라 이부분에 대한 내 이해가 정확한지는 모르겠지만 나름 해석을 해보자면 NLP에서 각 word token은 고정된 크기의 embedding으로 변환 된다. 하지만 이미지는 그 크기가(resolution이) 640x480, 1024X768등 다양할 수 있다. 따라서, 영상에서 NLP의 token과 같은 고정된 크기로 표현 가능한 단위를 설정하는게 필요하다.
-> 일정 한 수의 pixel 집합을 patch라고 정의하고 이 patch를 token처럼 처리의 최소 단위로 정의해 이 문제를 해결
2. 영상은 텍스트에 비해 high resolution이다.
semantic segmentation 같은 경우 pixel 단위의 prediction이 필요 한데 transformer의 computational complexity가 image size에 qudratic 하게 증가 하기 때문에 연산량 증가의 문제가 발생한다.
-> 계층적인 feature map을 이용하고 feature map의 window 내에서 local self-attention을 적용함으로서 complexity 문제를 해결, 각 window에는 일정한 수의 patch 만 포함되도록 설계하여 전체 연산량이 window 수에 선형적으로 증가하게 설계(self-attention 계산 방식의 최적화)
3. self-attention을 ResNet의 spatial convolution 전체 또는 일부를 대체하는 방식이 제안된 적이 있으나 실제 하드웨어에서 latency issue가 발생한다( 이부분은 정확히 이해 하지 못했다. 언급된 방식들의 caching 능력이 떨어진다고 봐야 할 거 같은데... 혹 이 글을 읽고 있는 누군가 이에 대한 답을 안다면 댓글로 설명 좀 해주심이..)
-> shift windows를 사용해 해결
즉 swin transformer 의 key feature는 1. shift window, hierahical patch representation(계층적 패치 표현), 최적화된 self-attention 계산 방식 으로 볼 수 있을거 같다.
구조
이제 swin transformer의 구조를 살펴 보자. 여기서는 아래 그림 Fig1 의 (d)의 전체 구조를 참고해 입력 영상이 각 모듈에 들어가서 연산을 거칠때 어떻게 변해 가는지 그리고 위의 contribution에서 언급한 각 문제점의 해결책이 어느 모듈에서 어떻게, 왜 수행되는지를 정리 할 것이다. 여기서는 숲을 설명하고 나무를 설명하는 방식이 아니라 각 모듈을 나무로 생각하고 나무에 대해서 설명한다. 각 모듈에 대한 설명을 이해하고 Fig1 (d)의 보면 전체적으로 이해 하는데 도움이 될 거라고 생각한다.
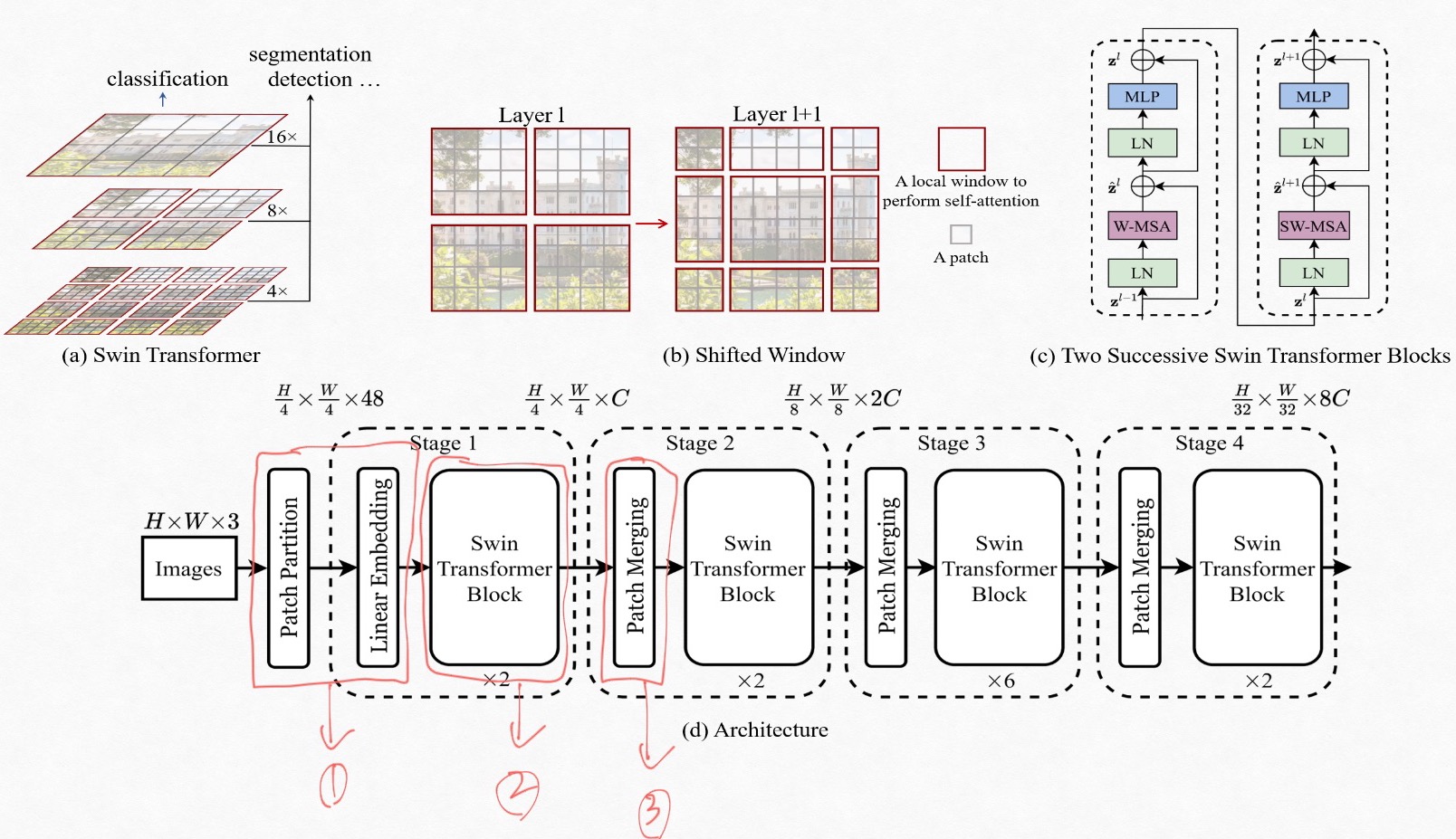
Fig1은 swin transformer 의 계측적 구조, shift window, transformer block 내부 구조, 전체 모델의 구조를 보여 준다. 우선 (d)의 전체 구조를 기준으로 살펴 보자.
swin transformer에서는 patch 라는 단위를 NLP의 token 처럼 사용한다. 이 patch를 이용해 고정된 크기의 embedding을 만들어 낸다. patch 라는 용어가 새로 나와 겁먹을 필요는 전혀 없다. 입력 영상에서 4x4 윈도우 내에 들어오는 pixel들을 concat해서 표현한 것이 patch이다.
예를 들어 입력 영상을 HxWx3, patch 크기를 4x4 pixel로 정하면, patch partition은 4x4 크기의 grid셀에서 그룹을 형성하는 pixel들을
| R | G | B | R | G | B | ... | G | B |
와 같이 concat해서 나타낸다. 이렇게 나타낸 patch는 4x4x3=48 의 크기를 지닌다. (4x4는 patch 크기 이고 3은 pixel의 channel 수 이다.) 이렇게 표현된 patch를 embedding으로 표현 하기 위해 linear layer를 이용해 연산한다.
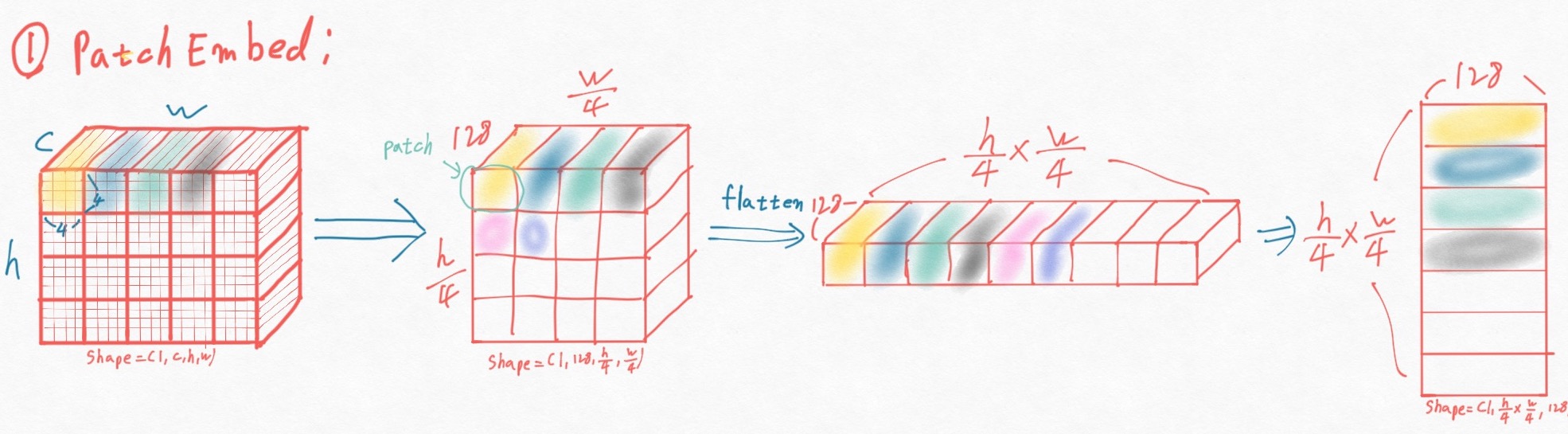
아래 그림 Fig2는 Fig 1. (d)의 patch partition + linear embedding 모듈에서 입력 영상이 어떠한 형태로 변화 되는 지를 간단히 도식화 하고 있다. Fig2 의 가장 좌측 그림을 보면 굵은 선 안쪽에 얇은 선으로 4x4 필셀을 표현했다. 서로 다른 색으로 표혀한 것이 4x4 pixel 그룹이다. 이 4x4 픽셀들을 channel 축으로 concat하고 128channel의 embedding 을 만들기 위해 linear layer에 입력하고 swin transformer block에 입력하기 위해 spatial 축(영상의 가로와 세로) 를 HxW 으로 flatten 해주면 Fig 2의 가장 오른쪽같은 형태가 된다.
다음으로 swin transformer block에서는 multihead attention을 이용한 연산을 수행한다. 블럭 내에서 수행되는 연산은 Fig 1의 (c)를 보면 알 쉽게 알수 있다. (c)에서 W-MSA는 윈도우 내에서 수행되는 multi head self-attention을 의미한고 SW-MSA는 shifted window multi head self-attention을 의미한다.
swin transformer에서 self attention은 non-overlapped window내의 patch만을 이용해 수행된다. 여기서 윈도우란 patch의 집합으로 이해 하면된다. (patch는 인접 pixel의 집합, window는 인접 patch의 집합)
W-MSA와 SW-MSA가 있는 이유는 input의 크기에 quadratic 하게 증가하는 computational complexity 문제를 해결하기 위해 도입한 window라는 개념 때문이다. 윗 문장에서 말했듯 swin transformer에서 정의하는 윈도우는 non-overlap이다. 즉 윈도우 내에 속한 patch 들 간의 연관성은 self-attention에서 고려 할수 있지만 서로 다른 윈도우에 속한 patch들 간의 연관성을 파악할 수 없다는 문제가 생긴다. 이를 해결 하기 위해 도입된게 SW-MSA(shifted window multi head self-attention)이다. Fig 1.의 (b)가 W-MSA와 SW-MSA에서 feature map을 어떻게 나누는지 보여준다. 우선 Fig 1. (b)의 왼쪽 그림은 사이즈가 4x4인 non-overlapped window로 feature map을 나눴을 때의 경우를 보여 준다(W-MSA에서 연산에 이용하는 window partition 방식이다.) Fig 1. (b)의 오른 쪽 그림은 SW-MSA모듈에서 사용하는 window partition 방식으로 W-MSA에서 서로 다른 window에 속해 있던 patch들이 같은 window로 묶이면서 상호간의 연관성(self-attention)을 고려 할 수 있게 된다.
SW-MSA를 구현 할때 한 가지 중요한 아이디어가 들어가는데 바로 cyclic shifted window이다. window의 크기와 shifted window의 stride에 따라 영상의 가장자리에 patch들이 window를 가득 채우지 못 할 경우 이를 해결 하기 위해 feature map을 단순히 패딩 하면 연산량이 증가되는 손실을 감수해야 한다. 저자는 이러한 문제를 효율적으로 풀기 위해 feature map을 top-left 방향으로 shift 시켰다. 아래 그림 Fig 3은 이 방식을 도식화해 보여 준다.

Fig 3 의 가장 왼쪽은 partition 된 feature map을 보여주는데 정 중앙에 위치한 M이 속한 윈도우만 실제 윈도우 크기에 부합하고 나머진 partition들은 윈도우의 크기보다 작게 된다. 각 partition을 모두 패딩해서 윈도우 크기인 4x4로 채우는 대신 Fig 3 cyclic shift 에 나타낸 것 처럼 A,B,C를 top-left 방향으로 회전(cyclic shift) 시키면 패딩을 하지 않아도(실제 코드에서는 물론 패딩도 들어간다. 하지만 패딩의 크기는 최소화 된다.) window 크기에 딱 맞는 partition을 만들 수 있다. 단 이렇게 하면 A,B,C는 원래의 feature map 에서 실제로는 서로 이웃 하지 않은 patch들과 같은 window에 속해 self-attention이 계산되는데 cyclic shift 하기 전의 feature map에서 서로 이웃 한 patch들간에만 self-attention이 계산 되도록 mask를 씌워준다. 이렇게 SW-MSA 연산이 끝나면 cyclic shift했던 것을 되돌려 준다.
W-MSA, SW-MSA에서 또 한가지 언급 할 것은 Relative position bias이다. Attention module 에서는 $\frac{Q \cdot K_{T}}{\sqrtd} +B$ 와 같이 positional bias (B) 를 연산 과정에서 더 해준다. swin transformer에서는 relative position bias를 이용했는데 윈도우 크기를 M 이라 할때 한 윈도우의 각 축으로 방향으로 $ [-M+1, M-1]$의 상대 위치 offset을 정의하고 이 값들로 B를 구성해 positional bias로 이용했다. (transformer에서 positional bias는 매우 중요한 개념이다. 여기선 간단히만 언급 했지만 사용 이유와 의미를 꼭 파악하자. 스스로에게 하는 말이다. )
아래 Fig 4. 은 Fig 1. (d)의 swin transformer block에서 입력이 data가 어떤 모양으로 변하고 어떻게 연산되는지를 간략히 도식화 한 그림이다. patch partition + linear embedding 단계에서 flatten되었던 입력 영상을 non-overlapped window로 분리하기 이해 공간 정보를 복원한다.(공간 정보를 복원한다는건 입력의 shape을 (batch size, HxW, embedding size)에서 (batch size, H,W, embedding size)로 reshape 하는 과정을 말한다.) 그 후 윈도우 크기로 분해된 feature map을 W-MSA또는 SW-MSA의 입력으로 넣어 attention 을 계산 해 준다. 어텐션 과정도 내 나름대로 도식화 했지만 내가 보기에만 좋은 그림 같기도 하다. 혹시 self-attention 연산 과정을 정확히 알지 못하는 독자는 여기 를 참조 하길 추천한다. (나에겐 정말 큰 도움이 되었다.)

그런데 왜 이렇게 window 개념을 도입하면 computational complexity가 줄어드는 걸까?
MSA 연산은 크게 다음과 같은 단계로 구성된다. -> 다음에 나오는 것은 각 단계에서 이루어지는 연산의 연산량이다.
1. input x와 weight $W_{Q}, W_{K}, W_{V}$를 이용해 $Q,K,V$ 계산
-> $Q = X \cdot W_{Q} => (hw \times C) \times (C \times C) = hw\times C^{2} $
$K = X \cdot W_{K} => (hw \times C) \times (C \times C) = hw\times C^{2}$
$V = X \cdot W_{V} => (hw \times C) \times (C \times C) = hw\times C^{2}$
2. $Q,K$ 를 이용해 attention score 구하기
-> $A = Q \cdot K^T => (hw\times C) \times (C \times hw) = (hw)^2C$
3. attention score와 $V$를 이용해 값 정재
-> $Z = A \cdot V =>(hw \times hw) \times (hw \times C) = hw\times C$
4. attention 적용된 output $Z$에 output weight $W_{z}$ 적용
-> $ out = Z \cdot W_{z} => (hw \times C) \times (C \times C) = hwC^2 $
이렇게 각 단계의 연산량을 다 더하면 MSA의 연산량은 $\Omega (MSA) = 4hwC^2 + 2(hw)^2C$ 이가 된다.
그럼 W-MSA 는 어떨까?
위에서 언급한 4단계에서 2, 3단계의 연산량이 아래와 같이 바뀐다.
2. $Q, K$ 를 이용해 attention score 구하기-> attention score를 윈도우 MxM에서 구하기
-> attention score를 구할때 고려하는 patch수는 hw가 아니라 MxM 즉 $M^2$
$A = Q \cdot K^T = (M^2 \times C) \times (C \times M^2) = M^{4}C$
3. attention score와 $V$를 이용해 값 정재
-> $ Z = A \cdot V => (M^2 \times M^2) \times (M^2 \times C) = M^{4}C$
다만 윈도우가 $\lfloor \frac{h}{M} \rfloor \times \lfloor \frac{w}{M} \rfloor $ 개 있으므로
$\frac{hw}{M^2} \times 2(M^4)C = 2M^2hwC$ 가 된다.
따라서 window multi head self-attention을 적용하면 $\Omega (W-MSA) = 4hwC^2 + 2M^2hwC$ 가 되어
$M^2 <= hw $ 일경우 연산량이 적어진다.
마지막으로 계층적(hierachical feature)를 생성하기 위해서 patch merging 모듈에서는 patch의 숫자를 줄인다. 방식은 patch partition 에서 input의 RGB 채널은 concat한 것 처럼
각 stage의 출력을 patch mergin layer에서 2x2 grid 안에 들어오는 즉 서로 인접한 4개의 patch를 채널 축으로 concat 해준다.
이걸 convolution의 receptive field관점으로 해석 하면 stage 1에서 4x4 가 receptive field이고 stage2dptjsms 8x8, stage 3 에서는 16x16, stage 4에서는 32x32 와 같이 볼 수 있다. Fig 1의 (a)는 이것을 도식화 한 것이다.
'Deeplearning > paperReviews' 카테고리의 다른 글
| [논문 리뷰] MobileViT 리뷰 (0) | 2022.06.24 |
|---|---|
| [논문 정리]CoordConv: An intriguing failing of convolution neural networks and the CoordConv solution 리뷰 (0) | 2021.08.10 |
| [InstanceSegmentation] SOLO:Segmenting Objects by Locations 논문 정리 (0) | 2021.08.08 |
| [ObjectDetection] FCOS(Fully Convolution One-Stage Detection) 논문 리뷰 (0) | 2021.05.30 |
| [AutoML] AttendNets 논문리뷰 (0) | 2021.05.19 |
